Assignment

Assignment: Matrix Algebra for Homogeneous & Non-Homogeneous Linear Algebraic System

The following linear algebraic equations, $[Q]\{c\}=\{b\}$ represents the 4 dof lake system, where RHS vector consists of the mass loading rate of chloride to each of the 4 lakes and $c_1$ , $c_2$ , $c_3$ and $c_4=$ the resulting chloride concentrations for Lakes Powell, Mead, Mohave, and Havasu, respectively.

\begin{bmatrix} q_{12}&0&0&0\\ -q_{12}&q_{23}&0&0\\ 0&-q_{23}&q_{34}&0\\ 0&0&-q_{34}&q_{44} \end{bmatrix} \begin{Bmatrix} c_1\\c_2\\c_3\\c_4 \end{Bmatrix} = \begin{Bmatrix} b_1\\b_2\\b_3\\b_4 \end{Bmatrix} = \begin{Bmatrix} 750.5\\300\\102\\30 \end{Bmatrix}

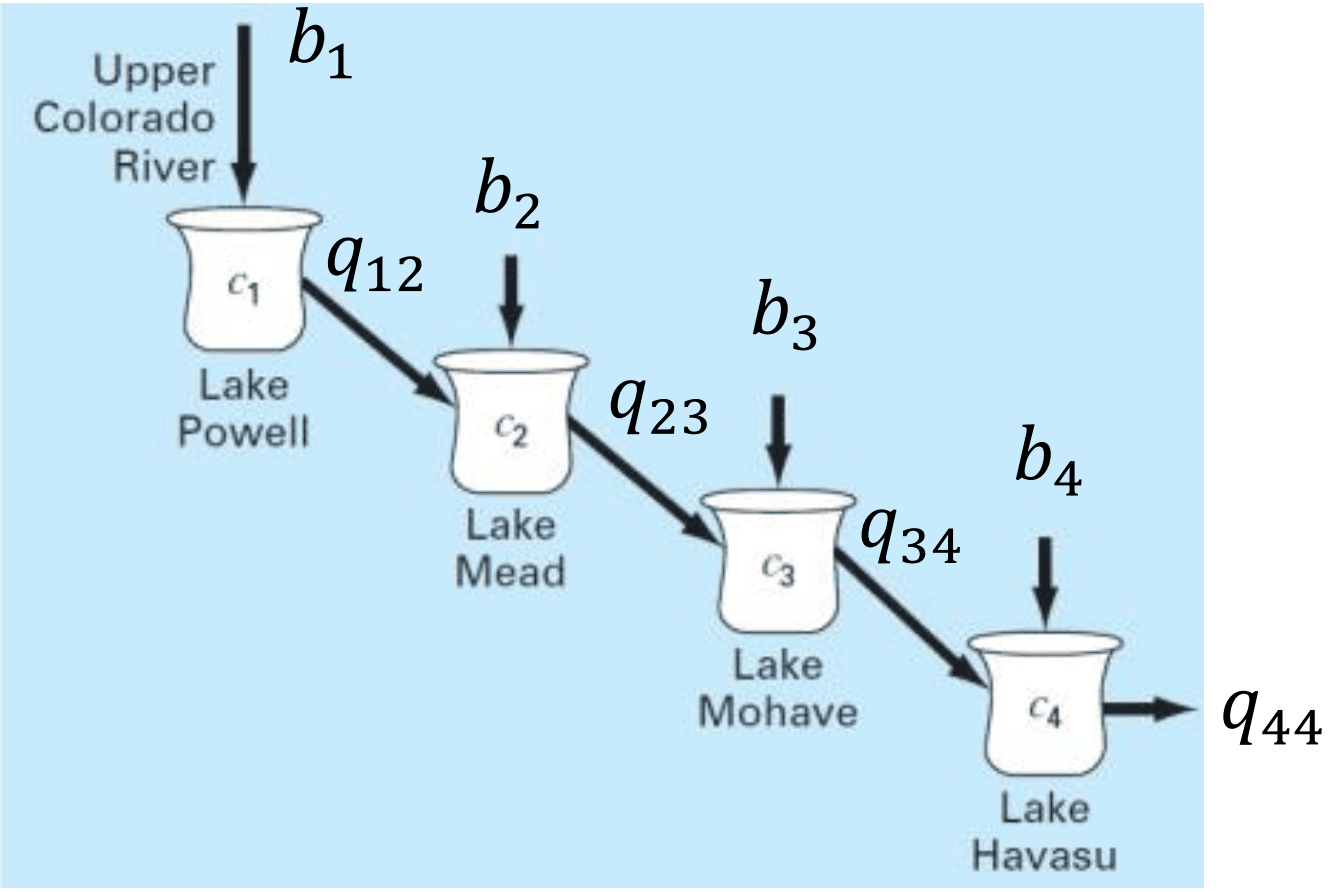
a. If the volumetric flow rates are given as follow: $q_{12} = 13.422$ , $q_{23} = 12.252$ , $q_{34} = 12.377$ and $q_{44} = 11.797$ . Use determinant analysis to check the condition of the system, then predict the characteristic of the solution without calculation.

(1 mark)

b. Solve the concentrations in each of the four lakes by using GEwPP method. The calculation must involve the scaling, partial pivoting, forward elimination and the backward substitution procedures.

(2 mark)

c. Discuss the advantage of GEwPP method and disadvantage of Cramer’s rule in terms of efficiency and accuracy for solving high dimension inverse problem with singular matrix.

(1 mark)

d. Obtain the eigenvalue matrix and normalized eigenvector matrix of the $[Q]$ . Note:Arrange the eigenvalue, $\lambda$ in ascending order $(\lambda_1<\lambda_2<\ldots<\lambda_n)$ .

(5 mark)

e. By using the result in (d), compute the matrix $\mathbf{K}$ indirectly by simplify the calculation using the following information: $\mathbf{Q}=\mathbf{K}^4$ , $(\mathbf{Q}-\lambda\mathbf{I})\mathbf{c}=0$ , eigenvalue property of $\mathbf{Q}^\mathbf{k}=\mathbf{P}\mathbf{D}^\mathbf{k}\mathbf{P}^{-1}$ .

\mathbf{K}= \begin{bmatrix} q_{12}&0&0&0\\ -q_{12}&q_{23}&0&0\\ 0&-q_{23}&q_{34}&0\\ 0&0&-q_{34}&q_{44} \end{bmatrix}^4 \begin{Bmatrix} c_1\\c_2\\c_3\\c_4 \end{Bmatrix}_{\lambda_3}

where $\{c\}_{\lambda_3} =$ normalized eigenvector of the 3rd eigenvalue (i.e 2nd largest)

(1 mark)

Your Help needed

This website has received 3000 view in the first two weeks! However, this project repository did not receive any star! Just simply head over to this website's repository to give it a star! Every tutorial takes me around two hours to compile, proof-read and styling this website! Your simple action would encourage me a lot! Thank you! You could Buy me a coffee too!