Tutorial 10

Tutorial 10: Multiple Integrals

Tutorial QuestionTutorial Solution

1. Evaluate the following:

   a. $\displaystyle\int_{1}^{2} \int_{2}^{3}(2 x-y) d y d x$

   Solution

   $$\begin{aligned} \int_1^2 \int_2^3(2 x-y) d y d x &=\int_1^2\left[(2 x) y-\left(\frac{y^2}{2}\right)\right]_2^3 d x \\ &=\int_1^2\left[\left((2 x)(3)-\frac{3^2}{2}\right)-\left((2 x)(2)-\frac{2^2}{2}\right)\right] d x \\ &=\int_1^2[(6 x-4.5)-(4 x-2)] d x=\int_1^2 2 x-2.5 d x \\ &=\left[x^2-2.5 x\right]_1^2=[(4-5)-(1-2.5)] \\ &=4-5-1+2.5=0.5 \end{aligned}$$

   b. $\displaystyle\int_{1}^{5} \int_{-1}^{2}(x-5 y) d x d y$

   Solution

   $$\begin{aligned} \int_1^5 \int_{-1}^2(x-5 y) d x d y &=\int_1^5\left[\frac{x^2}{2}-(5 y) x\right]_{-1}^2 d y \\ &=\int_1^5[(2-10 y)-(0.5+5 y)] d y=\int_1^5 1.5-15 y d y \\ &=\left[1.5 y-\frac{15 y^2}{2}\right]_1^5=[(7.5-187.5)-(1.5-7.5)]=-174 \end{aligned}$$

   c. $\displaystyle\int_{1}^{3} \int_{2}^{5}(2 x-3 y) d x d y$

   Solution

   $$\begin{aligned} \int_1^3 \int_2^5(2 x-3 y) d x d y&=\int_1^3\left[\frac{2 x^2}{2}-(3 y) x\right]_2^5 d y \\ &=\int_1^3\left[\left(5^2-3(5) y\right)-\left(2^2-3(2) y\right)\right] d y \\ &=\int_1^3[21-9 y] d y \\ &=\left[21 y-\frac{9 y^2}{2}\right]_1^3 \\ &=\left[\left(21(3)-\frac{9(3)^2}{2}\right)-\left(21(1)-\frac{9(1)^2}{2}\right)\right] \\ &=(63-40.5)-(21-4.5)=6 \end{aligned}$$

2. Evaluate each of the following integrals over the given region $D$ :

   a. $\displaystyle\iint_{D}\left(1-\frac{1}{2} x^{2}-\frac{1}{2} y^{2}\right) d A \quad$ where $\mathrm{D}$ is the region given by $0 \leq \mathrm{x} \leq 1,0 \leq \mathrm{y} \leq 1$

   Solution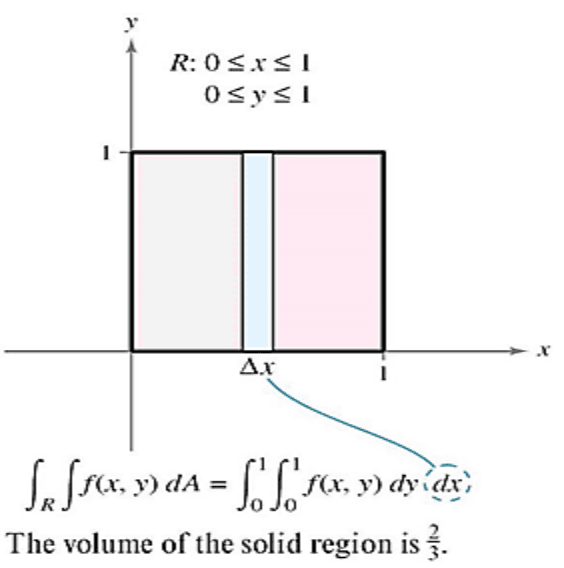

   

   • Because the region R is a square, it is both vertically and horizontally simple, and you can use either order of integration.
   • Choose $dy$ $dx$ by placing a vertical representative rectangle in the region, as shown in the figure at the right.

   $$\begin{aligned} \iint_R\left(1-\frac{1}{2} x^2-\frac{1}{2} y^2\right) d A &=\int_0^1 \int_0^1\left(1-\frac{1}{2} x^2-\frac{1}{2} y^2\right) d y d x \\ &=\int_0^1\left[\left(1-\frac{1}{2} x^2\right) y-\frac{y^3}{6}\right]_0^1 d x \\ &=\int_0^1\left(\frac{5}{6}-\frac{1}{2} x^2\right) d x \\ &=\left[\frac{5}{6} x-\frac{x^3}{6}\right]_0^1=\frac{2}{3} \end{aligned}$$

   b. $\displaystyle\iint_{D}\left(4 x y-y^{3}\right) d A \quad$ where $\mathrm{D}$ is the region given by $\mathrm{y}=\mathrm{x}^{0.5}$ and $\mathrm{y}=\mathrm{x}^{3}$

   Solution

   $$\begin{aligned} \iint_D\left(4 x y-y^3\right) d A \quad & 0 \leq x \leq 1 \text { and } x^3 \leq y \leq x^{0.5} \\ &=\int_0^1 \int_{x^3}^{x^{0.5}} 4 x y-y^3 d y d x \\ &=\int_0^1\left[\frac{4 x y^2}{2}-\frac{y^4}{4}\right]_{x^3}^{x^{0.5}} d x \\ &=\int_0^1\left[\left(\frac{4 x\left(x^{0.5}\right)^2}{2}-\frac{\left(x^{0.5}\right)^4}{4}\right)-\left(\frac{4 x\left(x^3\right)^2}{2}-\frac{\left(x^3\right)^4}{4}\right)\right] d x &=\int_0^1\left[\left(\frac{4 x^2}{2}-\frac{x^2}{4}\right)-\left(\frac{4 x^7}{2}-\frac{x^{12}}{4}\right)\right] d x \\ &=\int_0^1\left[\frac{7}{4} x^2-2 x^7+\frac{1}{4} x^{12}\right] d x \\ &=\left[\frac{7}{12} x^3-\frac{1}{4} x^8+\frac{1}{52} x^{13}\right]_0^1 \\ &=\frac{55}{156} \end{aligned}$$

3. Evaluate the following integral:

   $$\iint_{D} 42 y^{2}-12 x d A \quad \text { where } D=\left\{(x, y) \mid 0 \leq x \leq 4,(x-2)^{2} \leq y \leq 6\right\}$$
   Solution

   

   $$\begin{aligned} \iint_D 42 y^2-12 x d A &=\int_0^4 \int_{(x-2)^2}^6 42 y^2-12 x d y d x \\ &=\int_0^4\left[14 y^3-12 x y\right]_{(x-2)^2}^6 d x \\ &=\int_0^4 3024-72 x-14(x-2)^6+12 x(x-2)^2 d x \\ &=\int_0^4 3024-24 x-48 x^2+12 x^3-14(x-2)^6 d x \\ &=\left[3024 x-12 x^2-16 x^3+3 x^4-2(x-2)^7\right]_0^4 \\ &=11136 \end{aligned}$$

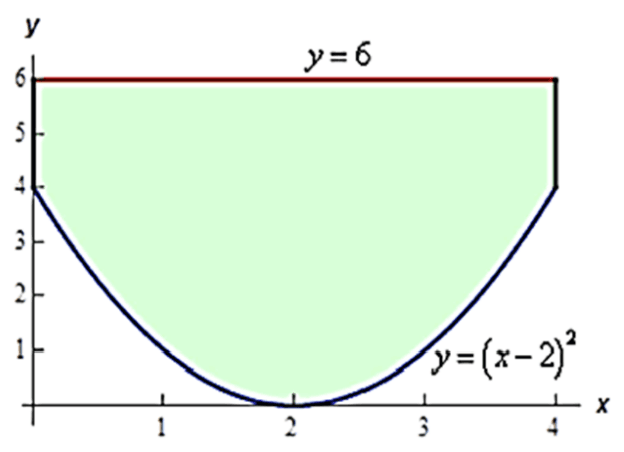
4. Evaluate the following integral over the indicated rectangle (a) by integrating with respect to $x$ first and (b) with respect to $y$ first.

   $$\iint_{R} 12 x-18 y d A \quad R=[-1,4] \times[2,3]$$
   Solution

   (a)

   $$\begin{aligned} \iint_R 12 x-18 y d A &=\int_2^3 \int_{-1}^4 12 x-18 y d x d y \\ &=\int_2^3\left[6 x^2-18 x y\right]_{-1}^4 d y=\int_2^3 90-90 y d y \\ &=\left[90 y-45 y^2\right]_2^3=-135 \end{aligned}$$

   (b)

   $$\begin{aligned} \iint_R 12 x-18 y d A &=\int_{-1}^4 \int_2^3 12 x-18 y d y d x \\ &=\int_{-1}^4\left[12 x y-9 y^2\right]_2^3 d x=\int_{-1}^4 12 x-45 d x \\ &=\left[6 x^2-45 x\right]_{-1}^4=-135 \end{aligned}$$

5. Compute the following double integral over the indicated rectangle

   a. $\displaystyle \iint_{R} 6 y \sqrt{x}-2 y^{3} d A \quad R=[1,4] \times[0,3]$

   Solution

   $$\begin{aligned} \iint_R 6 y \sqrt{x}-2 y^3 d A &=\int_0^3 \int_1^4 6 y x^{\frac{1}{2}}-2 y^3 d x d y \\ &=\left.\int_0^3\left(4 y x^{\frac{3}{2}}-2 x y^3\right)\right|_1 ^4 d y=\int_0^3 28 y-6 y^3 d y \\ &=\left.\left(14 y^2-\frac{3}{2} y^4\right)\right|_0 ^3=\frac{9}{2} \end{aligned}$$

   b. $\displaystyle\iint_{R} y e^{y^{2}-4 x} d A \quad R=[0,2] \times[0, \sqrt{8}]$

   Solution

   $$\begin{aligned} \iint_R 6 y \sqrt{x}-2 y^3 d A &=\int_0^3 \int_1^4 6 y x^{\frac{1}{2}}-2 y^3 d x d y \\ &=\left.\int_0^3\left(4 y x^{\frac{3}{2}}-2 x y^3\right)\right|_1 ^4 d y=\int_0^3 28 y-6 y^3 d y \\ &=\left.\left(14 y^2-\frac{3}{2} y^4\right)\right|_0 ^3=\frac{9}{2}\\ &=\left.\int_0^2\left(\frac{1}{2} e^{y^2-4 x}\right)\right|_0 ^{\sqrt{8}} d x=\int_0^2 \frac{1}{2}\left(e^{8-4 x}-e^{-4 x}\right) d x \\ &=\left.\left(\frac{1}{2}\left(-\frac{1}{4} e^{8-4 x}+\frac{1}{4} e^{-4 x}\right)\right)\right|_0 ^2 \\ &=\frac{1}{8}\left(e^8+e^{-8}-2\right)=372.3698 \end{aligned}$$

6. Evaluate:

   a. $\displaystyle\int_{-3}^{1} \int_{-1}^{2} \int_{0}^{1} 6 x y z d y d x d z$

   Solution

   $$\begin{aligned} \int_{-3}^1 \int_{-1}^2 \int_0^1 6 x y z d y d x d z &=\int_{-3}^1 \int_{-1}^2\left[3 x y^2 z\right]_0^1 d x d z \\ &=\int_{-3}^1 \int_{-1}^2 3 x z d x d z \\ &=\int_{-3}^1\left[\frac{3}{2} x^2 z\right]_{-1}^2 d z=\int_{-3}^1\left[6 z-\frac{3}{2} z\right] d z \\ &=\int_{-3}^1\left[\frac{9}{2} z\right] d z=\left[\frac{9}{4} z^2\right]_{-3}^1 \\ &=\frac{9}{4}-\frac{9}{4}(9)=\frac{9}{4}-\frac{81}{4} \\ &=\frac{-72}{4}=-18 \end{aligned}$$

   b. $\displaystyle \int_{0}^{4} \int_{-2}^{-1} \int_{1}^{2} x y d x d y d z$

   Solution

   $$\begin{aligned} \int_0^4 \int_{-2}^{-1} \int_1^2 x y d x d y d z &=\int_0^4 \int_{-2}^{-1}\left[\frac{x^2}{2} y\right]_1^2 d y d z=\int_0^4 \int_{-2}^{-1} 1.5 y d y d z \\ &=\int_0^4\left[\frac{1.5 y^2}{2}\right]_{-2}^{-1} d z=\int_0^4-2.25 d z \\ &=[-2.25 z]_0^4=-9 \end{aligned}$$

7. Evaluate:

   a. $\displaystyle\iiint_{B} x y z^{2} d V\qquad\begin{aligned} &0 \leq x \leq 1 \\ &-1 \leq y \leq 2 \\ &0 \leq z \leq 3\end{aligned}$

   Solution

   $$\begin{aligned} \iiint_{B} x y z^{2} d V&=\int_0^3 \int_{-1}^2 \int_0^1 x y z^2 d x d y d z\\ &=\int_0^3 \int_{-1}^2\left[\frac{x^2 y z^2}{2}\right]_{x=0}^{x=1} d y d z=\int_0^3 \int_{-1}^2 \frac{y z^2}{2} d y d z\\ &=\int_0^3\left[\frac{y^2 z^2}{4}\right]_{y=-1}^{y=2} d z=\int_0^3 \frac{3 z^2}{4} d z\\ &=\left[\frac{z^3}{4}\right]_0^3=\frac{27}{4} \end{aligned}$$

   b. $\displaystyle\iiint_{B} 4x^2y-z^3 dz dy dx \qquad\begin{aligned} &2 \leq x \leq 3 \\ &-1 \leq y \leq 4 \\ &0 \leq z \leq 1\end{aligned}$

   Solution

   $$\begin{aligned} \iiint_{B} 4x^2y-z^3 dz dy dx&=\int_2^3 \int_{-1}^4\left[4 x^2 y z-\frac{1}{4} z^4\right]_0^1 d y d x \\ &=\int_2^3 \int_{-1}^4\left[4 x^2 y z-\frac{1}{4} z^4\right]_0^1 d y d x \\ &=\int_2^3 \int_{-1}^4 \frac{1}{4}-4 x^2 y d y d x \\ &=\int_2^3\left[\frac{1}{4} y-2 x^2 y^2\right]_{-1}^4 d x=\int_2^3 \frac{5}{4}-30 x^2 d x \\ &=\left[\frac{5}{4} x-10 x^3\right]_2^3=-\frac{755}{4} \end{aligned}$$

8. Integrate the function $(x, y, z)=x y$ over the volume enclose by the planes $z=x+y$ and $z=0$, and between the surfaces $y=x^{2}$ and $x=y^{2}$.

   Solution

   Since $z$ is expressed as a function of $(x, y)$, the integration is done in the $z$ direction first. Considering the $xy$-plane, the two curves meet at $(0, 0)$ and $(1, 1)$. The integral is:

   $$\begin{aligned} \int_0^1 \int_{x^2}^{\sqrt{x}} \int_0^{x+y} f(x, y, z) d z d y d x &=\int_0^1 \int_{x^2}^{\sqrt{x}} \int_0^{x+y} x y d z d y d x \\ &=\int_0^1 \int_{x^2}^{\sqrt{x}} x y[z]_{z=0}^{z=x+y} d y d x \\ &=\int_0^1 \int_{x^2}^{\sqrt{x}} x y(x+y) d y d x \int_0^1 \int_{x^2}^{\sqrt{x}} x^2 y+y^2 x d y d x \\ &=\int_0^1\left[\frac{x^2 y^2}{2}+\frac{y^3 x}{3}\right]_{y=x^2}^{y=\sqrt{x}} d x \\ &=\frac{1}{2} \int_0^1\left(x^2 \sqrt{x}{ }^2-x^2\left(x^2\right)^2\right) d x \\ &=\frac{1}{2} \int_0^1\left(x^3-x^6\right) d x+\frac{1}{3} \int_0^1\left(\sqrt{x} x-\left(x^2\right)^{\frac{5}{2}}-x^7\right) d x \\ &=\frac{1}{2}\left[\frac{x^4}{4}-\frac{x^7}{7}\right]_0^1+\frac{1}{3}\left[\frac{2 x^{\frac{7}{2}}}{7}-\frac{x^8}{8}\right]_0^1 \\ &=\frac{1}{2}\left(\frac{1}{4}-\frac{1}{7}\right)+\frac{1}{3}\left(\frac{2}{7}-\frac{1}{8}\right)=\frac{3}{28} \end{aligned}$$

9. Find the mass for the following square lamina, represented by the unit square (shown below) with variable density $\rho(x, y)=(x+y+2) \mathrm{g} / \mathrm{cm}^{2}$.

   

   Figure 1. A region R representing a lamina

   Solution

   $$\begin{aligned} M=\iint_R(x+y+2) d A &=\int_0^1 \int_0^1(x+y+2) d x d y \\ &=\int_0^1\left[\frac{1}{2} x^2+x(y+2)\right]_0^1 d y \\ &=\int_0^1 \frac{5}{2}+y d y \\ &=\left[\frac{5}{2} y+\frac{y^2}{2}\right]_0^1 \\ &=\frac{5}{2}+\frac{1}{2} \\ &=3 g \end{aligned}$$

10. Find the mass and center of mass for the following solid region $Q$ bounded by $x+2 y+3 z$ $=6$ and the coordinate planes (as shown below) and has density $\rho(x, y, z)=x^{2} y z$.

    

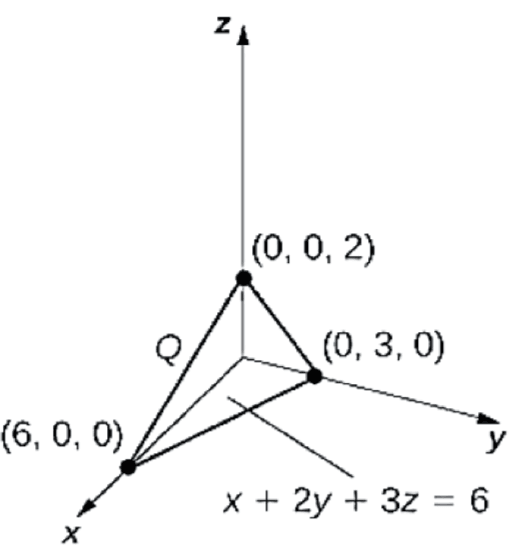
    Figure 2: Finding the mass of a three-dimensional solid Q.

    Solution

    The region $Q$ is a tetrahedron meeting the axes at the points $(6,0,0),(0,3,0)$ and $(0,0,2)$. To find the limits of integration, let $z=0$ in the slated plane $z=\frac{1}{3}(6-x-2 y)$.

    Then for $x$ and $y$, find the projection of $Q$ onto the $x y$-plane, which is bounded by the axes and the line $x+2 y=6$. Therefore, the mass $(m)$ is:

    $$\begin{aligned} m=\iiint_Q \rho(x, y, z) d V &=\int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}\left(6-x_{-}\right.} \int_{z=0}^{z=\frac{1}{3}(6-x-2 y)} x^2 y z d z d y d x \\ &=\frac{108}{35} \end{aligned}$$

    To find the center of mass of $\mathrm{Q}$, we need to find the moments about the $x y$-plane, the $x z$-plane and the $y z$-plane:

    $$\begin{aligned} M_{x y}&=\iiint_Q z \rho(x, y, z) d V&&=\int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2 y)} x^2 y z^2 d z d y d x\\ &&&=\frac{54}{35} \\\\ M_{x z}&=\iiint_Q y \rho(x, y, z) d V&&=\int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2 y)} x^2 y^2 z d z d y d x\\ &&&=\frac{81}{35}\\\\ M_{y z}&=\iiint_Q x \rho(x, y, z) d V&&=\int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2 y)} x^3 y z d z d y d x\\ &&&=\frac{243}{35} \end{aligned}$$

    Hence the center of mass is:

    $$\begin{aligned} \bar{x}&=\frac{M_{y z}}{m} & \bar{y}&=\frac{M_{x z}}{m} & \bar{z}&=\frac{M_{x y}}{m} \\ \bar{x}&=\frac{M_{y z}}{m}=\frac{243 / 35}{108 / 35}=\frac{243}{108} & \bar{y}&=\frac{M_{x z}}{m}=\frac{81 / 35}{108 / 35}=\frac{81}{108} & \bar{y}&=\frac{M_{x y}}{m}=\frac{54 / 35}{108 / 35}=\frac{54}{108} \\ &=2.25 & &=0.75 & &=0.5 \end{aligned}$$

    The center of mass: $\quad(2.25,0.75,0.5)$