Skip to main content

Tutorial 13

Tutorial 13: Surface Integrals

  1. Evaluate the surface integral of the vector field F=3x2i−2yxj+8k\mathbf{F}=3 x^{2} \mathbf{i}-2 y x \mathbf{j}+8 \mathbf{k} over the surface SS that is the graph of z=2x−yz=2 x-y over the rectangle [0,2]×[0,2][0,2] \times[0,2].

    Solution

    Use the formula for a surface integral over a graph z=g(x,y)z=g(x,y):

    ∬SF⋅dS=∬D[F⋅(−∂g∂xi−∂g∂yj+k)]dxdy\begin{equation*} \iint_S\mathbf{F}\cdot d\mathbf{S}=\iint_D\left[\mathbf{F}\cdot\left(-\frac{\partial g}{\partial x}\mathbf{i}-\frac{\partial g}{\partial y}\mathbf{j}+\mathbf{k}\right)\right]dxdy \end{equation*}

    For z=2x−yz=2x-y →\rightarrow −2x+y+z=0-2x+y+z=0, therefore,

    ∫02∫02(3x2,−2yx,8)⋅(−2,1,1)dxdy=∫02∫02(−6x2−2yx+8)dxdy=∫02−2x3−yx2+8x∣x=02dy=∫02−4ydy=−2y2∣02=−8\begin{equation*} \begin{aligned} \int_0^2\int_0^2(3x^2,-2yx,8)\cdot(-2,1,1)dxdy&=\int_0^2\int_0^2(-6x^2-2yx+8)dxdy\\ &=\int_0^2\left.-2x^3-yx^2+8x\right|_{x=0}^2dy\\ &=\int_0^2-4ydy\\ &=\left.-2y^2\right|_0^2=-8 \end{aligned} \end{equation*}

  2. Let SS be the triangle with vertices (1,0,0),(0,2,0)(1,0,0),(0,2,0) and (0,1,1)(0,1,1) and let F=xyz(i+j)\mathbf{F}=x y z(\mathbf{i}+\mathbf{j}). calculate the surface integral

    ∬SF⋅dS\iint_{S} F \cdot d \mathbf{S}

    If the triangle is oriented by the "downward" normal.

    Solution

    Since SS lies in a plane, it is part of the graph of a linear function z=ax+by+cz=ax+by+c.

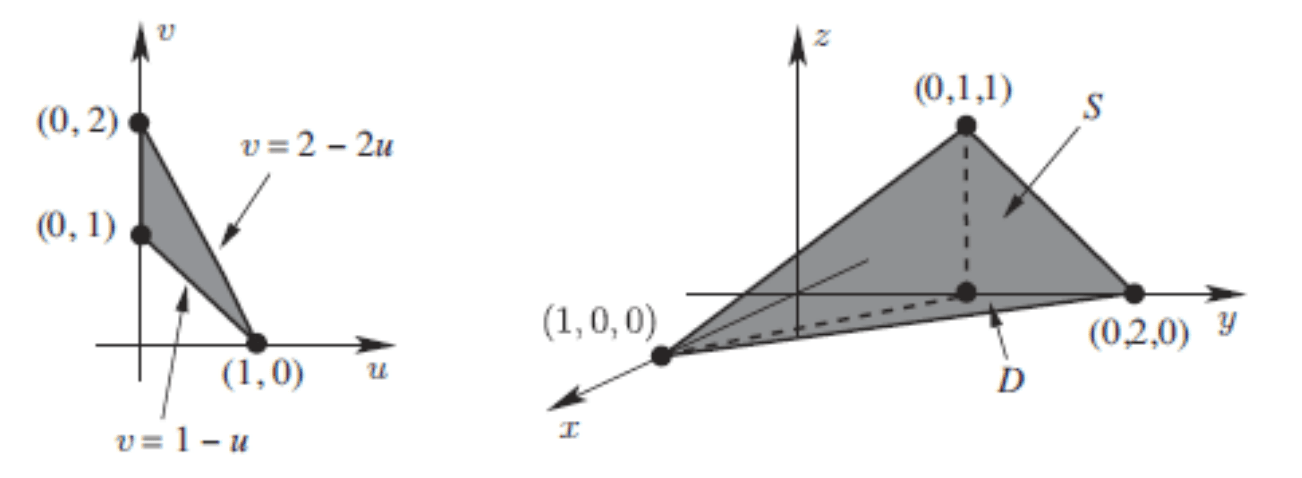
    Figure for Question 2

    Substituting the vertices of the triangle for (x,y,z)(x,y,z), we get the equation

    0=a+c,0=2b+c,1=b+c0=a+c,\quad0=2b+c,\quad1=b+c

    which we can solve to find b=−1b=-1, =2=2, a=−2a=-2, i.e., z=−2x−y+2z=-2x-y+2. We may take xx and yy as parameters,

    x=u,y=v,z=−2u−v+2x=u,\quad y=v,\quad z=-2u-v+2

    or Φ(u,v)=(u,v,−2u−v+2)\mathbf{\Phi}(u,v)=(u,v,-2u-v+2). The domain DD of the parametrization is the triangle with vertices at (1,0)(1,0), (0,2)(0,2), and (0,1)(0,1) in the (u,v)(u,v) plane. For this parametrization,

    Tu×Tv=(1,0,−2)×(0,1,−1)=(2,1,1)\mathbf{T}_u\times\mathbf{T}_v=(1,0,-2)\times(0,1,-1)=(2,1,1)

    Since the third component of this vector is positive, the orientation determined by Φ\mathbf{\Phi} is ``upward'', so we will have to multiply our find answer by −1-1 to get the surface integral with the \textbf{downward} orientation.

    Now, we have (with the minus sign reminding us that the orientation is wrong),

    −∬SF⋅dS=∬Dxyz(i+j)⋅(2i+j+k)dudv=∬D3xyzdudv=∬D3uv(−2u−v+2)dudv\begin{equation*} \begin{aligned} -\iint_S\mathbf{F}\cdot d\mathbf{S}&=\iint_D xyz(\mathbf{i}+\mathbf{j})\cdot(2\mathbf{i}+\mathbf{j}+\mathbf{k})dudv\\ &=\iint_D3xyzdudv\\ &=\iint_D3uv(-2u-v+2)dudv \end{aligned} \end{equation*}

    To compute the double integral, we draw the integtation domain DD in the uvuv-plane, in the left hand part of the Figure. By reduction to iterated integrals,

    ∬D3uv(−2u−v+2)dudv=∫01∫1−u2−2u(−6u2v−3uv2+6uv)dvdu\iint_D3uv(-2u-v+2)dudv=\int_0^1\int_{1-u}^{2-2u}(-6u^2v-3uv^2+6uv)dvdu

    Carrying out the vv-integration, we get

    ∫01[−3u2v2−uv3+3uv2]∣1−u2−2udu=∫01uv2[−3u−v+3]∣1−u2(1−u)du=∫01[4u(1−u)2(1−u)−u(1−u)22(1−u)]du=2∫01u(1−u)3du=2∫01(u−3u2+3u3−u4)du=2(12−33+34−15)=110\begin{equation*} \begin{aligned} &\int_0^1\left.\left[-3u^2v^2-uv^3+3uv^2\right]\right|_{1-u}^{2-2u}du\\ &=\int_0^1\left.uv^2[-3u-v+3]\right|_{1-u}^{2(1-u)}du\\ &=\int_0^1\left[4u(1-u)^2(1-u)-u(1-u)^22(1-u)\right]du\\ &=2\int_0^1u(1-u)^3du\\ &=2\int_0^1(u-3u^2+3u^3-u^4)du\\ &=2\left(\frac{1}{2}-\frac{3}{3}+\frac{3}{4}-\frac{1}{5}\right)=\frac{1}{10} \end{aligned} \end{equation*}
    ∴∬SF⋅dS=−110\therefore\iint_S\mathbf{F}\cdot d\mathbf{S}=-\frac{1}{10}

  3. The equations z=12,x2+y2≤25z=12, x^{2}+y^{2} \leq 25 describe a disk of radius 5 lying in the plane z=12z=12. Suppose that is the position vector field r(x,y,z)=xi+yj+zk\mathbf{r}(x, y, z)=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}. Compute ∬Sr.dS\iint_{S} \mathbf{r} . d \mathbf{S}.

    Solution

    Since the disk is parallel to the xyxy plane, the outward unit normal is k\mathbf{k}. Hence n(x,y,z)=k\mathbf{n}(x, y, z) = \mathbf{k} and so r⋅n=z\mathbf{r}\cdot \mathbf{n} = z. Thus,

    ∬Sr⋅dS=∬Sr⋅ndS=∬SzdS=∬D12dxdy=300π\iint_S\mathbf{r}\cdot d\mathbf{S}=\iint_S\mathbf{r}\cdot\mathbf{n}dS=\iint_SzdS=\iint_D12dxdy=300\pi

    Alternatively we may solve this problem by using the formula for surface integrals over graphs:

    ∬SF⋅dS=∬DF⋅(−∂g∂xi−∂g∂yj+k)dxdy\iint_S\mathbf{F}\cdot d\mathbf{S}=\iint_D\mathbf{F}\cdot\left(-\frac{\partial g}{\partial x}\mathbf{i}-\frac{\partial g}{\partial y}\mathbf{j}+\mathbf{k}\right)dxdy

    With g(x,y)=12g(x,y)=12 and DD the disk x2+y2≤25x^2+y^2\leq25, we get

    ∬SF⋅dS=∬D(x⋅0+y⋅0+12)dxdy=12(area of D)=300π\iint_S\mathbf{F}\cdot d\mathbf{S}=\iint_D(x\cdot0+y\cdot0+12)dxdy=12(\text{area of }D)=300\pi

  4. Let SS be the closed surface that consists of the hemisphere x2+y2+z2=1≥0x^{2}+y^{2}+z^{2}=1 \geq 0, and its base x2+y2≤1,z=0x^{2}+y^{2} \leq 1, z=0. Let EE be the electric field defined by E(x,y,z)=2xi+2yj+2zk\mathbf{E}(x, y, z)=2 x \mathbf{i}+2 y \mathbf{j}+2 z \mathbf{k}. Find the electric flux across SS.

    Solution

    Write S=H∪DS = H \cup D where HH is the upper hemisphere and DD is the disk. Hence

    ∬SE⋅dS=∬HE⋅dS+∬DE⋅dS\iint_S\mathbf{E}\cdot d\mathbf{S}=\iint_H\mathbf{E}\cdot d\mathbf{S}+\iint_D\mathbf{E}\cdot d\mathbf{S}

    Let xi+yj+zkx\mathbf{i} + y\mathbf{j} + z\mathbf{k} be the unit normal nn pointing outward from HH. Then

    ∬HE⋅dS=∬HE⋅ndS=∬H(2x,2y,2z)⋅(x,y,z)dS=2∬H(x2+y2+z2)dS=2∬HdS=4π\begin{equation*} \begin{aligned} \iint_H\mathbf{E}\cdot d\mathbf{S}&=\iint_H\mathbf{E}\cdot\mathbf{n}dS\\&=\iint_H(2x,2y,2z)\cdot(x,y,z)dS\\ &=2\iint_H(x^2+y^2+z^2)dS\\ &=2\iint_HdS=4\pi \end{aligned} \end{equation*}

    The unit normal is −k-\mathbf{k} and z=0z = 0 on DD. Hence,

    ∬DE⋅dS=∬DE⋅ndS=∬D(2x,2y,2z)⋅(0,0,−1)dS=0\iint_D\mathbf{E}\cdot d\mathbf{S}=\iint_D\mathbf{E}\cdot\mathbf{n}dS=\iint_D(2x,2y,2z)\cdot(0,0,-1)dS=0

    Therefore,

    ∬SE⋅dS=4π\iint_S\mathbf{E}\cdot d\mathbf{S}=4\pi

  5. Find the area of the ellipse cut on the plane 2x+3y+6z=602 x+3 y+6 z=60 by the circular cylinder x2+y2=2xx^{2}+y^{2}=2 x.

    Solution

    The surface SS lies in the plane 2x+3y+6z=602x+3y+6z = 60 so we use this to calculate dS=1+(∂z∂x)2+(∂z∂y)2dxdydS =\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2}dxdy. Differentiating the equation for the plane with respect to xx gives,

    2+6∂z∂x=0⇒∂z∂x=−132+6\frac{\partial z}{\partial x}=0\quad\Rightarrow\quad \frac{\partial z}{\partial x}=-\frac{1}{3}

    Differentiating the equation for the plane with respect to yy gives,

    3+6∂z∂y=0⇒∂z∂y=−123+6\frac{\partial z}{\partial y}=0\quad\Rightarrow\quad\frac{\partial z}{\partial y}=-\frac{1}{2}

    Hence,

    1+(∂z∂x)2+(∂z∂y)2=1+19+14=76\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2}=\sqrt{1+\frac{1}{9}+\frac{1}{4}}=\frac{7}{6}

    Then the area of SS is found be calculating the surface integral over SS for the function f(x,y,z)=1f(x, y, z) = 1. The projection of the surface, SS, onto the xy-plane is given by D={(x,y):x2−2x+y2=(x−1)2+y2≤1}D=\{(x, y) : x^2 - 2x + y^2 = (x - 1)^2 + y^2 \leq 1\}. Hence the area of SS is given by

    ∬S1dS=∬D1⋅76dxdy=76∬D1dxdy=76×Area of D=76π\begin{equation*} \begin{aligned} \iint_S1dS&=\iint_D1\cdot\frac{7}{6}dxdy\\ &=\frac{7}{6}\iint_D1dxdy\\ &=\frac{7}{6}\times\text{Area of }D\\ &=\frac{7}{6}\pi \end{aligned} \end{equation*}

    Note, since DD is a circle or radius 1 centred at (1,0)(1, 0) the area of DD is the area of a unit circle which is π\pi.

  6. Find the integral ∬SxdS\iint_{S} x d S, where the surface SS is the part of the sphere x2+y2+z2=a2x^{2}+y^{2}+z^{2}=a^{2} lying in the first octant.

    Solution

    It is convenient to solve this integral in spherical coordinates. The area element for spherical surface is dS=a2sin⁡θdϕdθdS=a^2\sin \theta d\phi d\theta. As x=acos⁡ϕsin⁡θx=a\cos\phi\sin\theta, we can write the integral in the following form

    I=∬SxdS=∬D(ϕ,θ)acos⁡ϕsin⁡θ⋅a2sin⁡θdϕdθ=a3∬D(ϕ,θ)cos⁡ϕsin⁡2θdϕdθ\begin{equation*} \begin{aligned} I=\iint_SxdS&=\iint_{D(\phi,\theta)}a\cos\phi\sin\theta\cdot a^2\sin\theta d\phi d\theta\\ &=a^3\iint_{D(\phi,\theta)}\cos\phi\sin^2\theta d\phi d\theta \end{aligned} \end{equation*}

    The domain of integration D(ϕ,θ)D(\phi,\theta) is defined as

    D={(ϕ,θ)∣0≤ϕ≤π2,0≤θ≤π2}D=\left\{(\phi,\theta)|0\leq\phi\leq\frac{\pi}{2},0\leq\theta\leq\frac{\pi}{2}\right\}

    Hence, the integral is

    I=a3∬D(ϕ,θ)cos⁡ϕsin⁡2θdϕdθ=a3∫0π2cos⁡ϕdϕ∫0π2sin⁡2θdθ=a3⋅[(sin⁡ϕ)∣0π2]⋅∫0π21−cos⁡2θ2dθ=a3⋅1⋅12∫0π2(1−cos⁡2θ)dθ=a32[(θ−sin⁡2θ2)∣0π2]=a32⋅π2=πa34\begin{equation*} \begin{aligned} I&=a^3\iint_{D(\phi,\theta)}\cos\phi\sin^2\theta d\phi d\theta\\ &=a^3\int_0^{\frac{\pi}{2}}\cos\phi d\phi\int_0^{\frac{\pi}{2}}\sin^2\theta d\theta\\ &=a^3\cdot\left[\left.(\sin\phi)\right|_0^{\frac{\pi}{2}}\right]\cdot\int_0^{\frac{\pi}{2}}\frac{1-\cos 2\theta}{2}d\theta\\ &=a^3\cdot 1\cdot\frac{1}{2}\int_0^{\frac{\pi}{2}}(1-\cos 2\theta)d\theta\\ &=\frac{a^3}{2}\left[\left.\left(\theta-\frac{\sin 2\theta}{2}\right)\right|_0^{\frac{\pi}{2}}\right]\\ &=\frac{a^3}{2}\cdot\frac{\pi}{2}=\frac{\pi a^3}{4} \end{aligned} \end{equation*}

  7. Find the integral ∬SdSx2+y2+z2\iint_{S} \frac{d S}{\sqrt{x^{2}}+y^{2}+z^{2}}, where SS is the part of the cylindrical surface parameterized by r(u,v)=(acos⁡u,asin⁡u,v),0≤u≤2π,0≤v≤Hr(u, v)=(a \cos u, a \sin u, v), 0 \leq u \leq 2 \pi, 0 \leq v \leq H.

    Solution

    Calculate the partial derivatives,

    ∂r∂u=(∂x∂u,∂y∂u,∂z∂u)=(−asin⁡u,acos⁡u,0)∂r∂v=(∂x∂v,∂y∂v,∂z∂v)=(0,0,1)\begin{equation*} \begin{aligned} \frac{\partial \mathbf{r}}{\partial u}&=\left(\frac{\partial x}{\partial u},\frac{\partial y}{\partial u},\frac{\partial z}{\partial u}\right)=(-a\sin u,a\cos u,0)\\ \frac{\partial \mathbf{r}}{\partial v}&=\left(\frac{\partial x}{\partial v},\frac{\partial y}{\partial v},\frac{\partial z}{\partial v}\right)=(0,0,1) \end{aligned} \end{equation*}

    and their cross product,

    ∂r∂u×∂r∂v=∣ijk−asin⁡uacos⁡u0001∣=acos⁡u⋅i+asin⁡u⋅j+0⋅k\frac{\partial \mathbf{r}}{\partial u}\times\frac{\partial \mathbf{r}}{\partial v}=\left|\begin{matrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\-a\sin u&a\cos u&0\\0&0&1\end{matrix}\right|=a\cos u\cdot\mathbf{i}+a\sin u\cdot\mathbf{j}+0\cdot\mathbf{k}

    Then the area element of the given surface is

    dS=∣∂r∂u×∂r∂v∣dudv=∣(acos⁡u)2+(asin⁡u)2∣dudv=adudvdS=\left|\frac{\partial\mathbf{r}}{\partial u}\times\frac{\partial\mathbf{r}}{\partial v}\right|dudv=\left|\sqrt{(a\cos u)^2+(a\sin u)^2}\right|dudv=adudv

    Now we can calculate the surface integral:

    ∬SdSx2+y2+z2=∬D(u,v)adudv(acos⁡u)2+(asin⁡u)2+v2=∬D(u,v)adudva2+v2=∫02πadu∫0Hdva2+v2=2πa∫0Hdva2+v2=2πa[ln⁡(v+a2+v2)∣v=0H]=2πa\begin{equation*} \begin{aligned} \iint_S\frac{dS}{\sqrt{x^2+y^2+z^2}}&=\iint_{D(u,v)}\frac{adudv}{\sqrt{(a\cos u)^2+(a\sin u)^2+v^2}}\\ &=\iint_{D(u,v)}\frac{adudv}{\sqrt{a^2+v^2}}\\ &=\int_0^{2\pi}adu\int_0^H\frac{dv}{\sqrt{a^2+v^2}}\\ &=2\pi a\int_0^H \frac{dv}{\sqrt{a^2+v^2}}\\ &=2\pi a\left[\left.\ln\left(v+\sqrt{a^2+v^2}\right)\right|_{v=0}^H\right]=2\pi a \end{aligned} \end{equation*}
    [ln⁡(H+a2+H2)−ln⁡a]=2πaln⁡H+a2+H2a\left[\ln\left(H+\sqrt{a^2+H^2}\right)-\ln a\right]=2\pi a\ln\frac{H+\sqrt{a^2+H^2}}{a}