Tutorial 12
Tutorial 12: Line Integrals
If , evaluate from to along the following paths :
a. .
Solutionb. The straight line from to then to , and then to .
SolutionFrom to ,
From to ,
From to ,
c. The straight line joining and .
Solution
Find the work done in moving a particle in a force field given by along the curve from to .
SolutionDetermine the work done in moving a particle counterclockwise once around a circle in the -plane, if the circle has center at the origin and radius of 3 and if those field is given by
Solution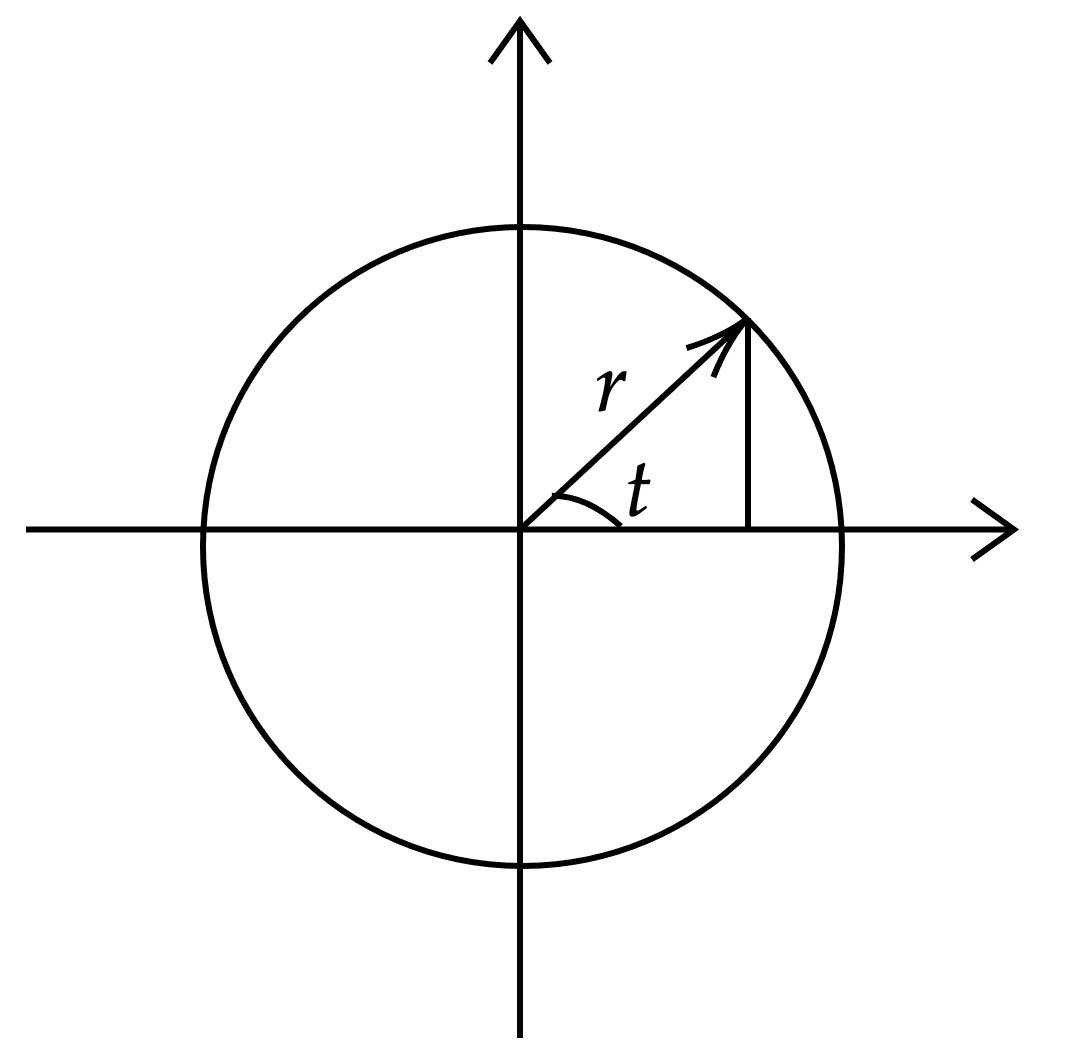
In the plane ,
The work done is,
Parametric equation of the circle: , , where varies from to .
The line integral,
Note: We choose counterclockwise direction, which is known as positive direction. If traversing from counterclockwise (negative) direction, the value of integral would be .
Find the line integral for where is the closed curve of the region bounded by and in the positive direction in traversing C. and intersect at and .
Solution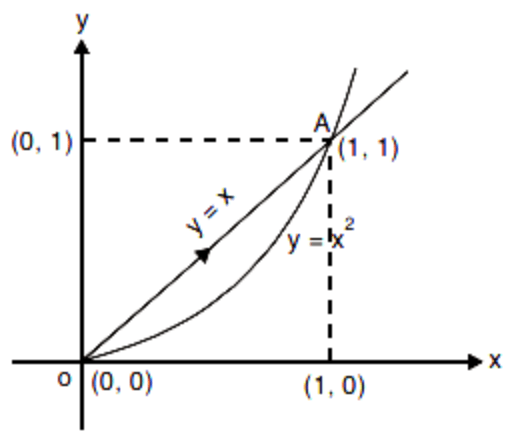
Along , where the line integral equals
Along from to , the line integral equals
L.H.S =
L.H.S = R.H.S = .
Evaluate where is the triangle of the figure below.
Solution, , , ,
Note: Although there exist lines parallel to the coordinate axes (coincident with the coordinate axes in this case) which meet in an infinite number of points, Green’s theorem in the plane still holds. In general the theorem is valid when is composed of a finite number of straight line segments.
Calculate where is the circle of radius 2 centered on the origin.
SolutionWe let and to get
Compute the line integral of along the path shown below against a grid of unit-sized squares.
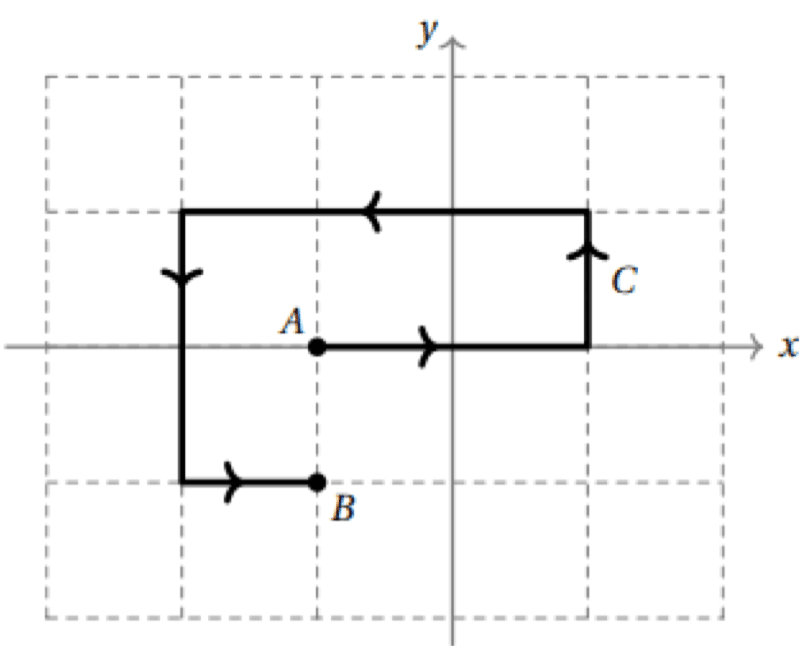 Solution
SolutionLet be the line segment going from to . Then, we can now apply Green’s theorem to combination of and . Let be the region bounded by these two paths. Then, by Green’s theorem, since we are oriented correctly,
because the area of the region is made of exactly 4 unit squares. The boundary of is and :
The line integral along is easier: parametrizing by for , we get
Putting it together,
A particle starts at and moves along the -axis to . Then it moves along the upper part of the circle and back to . Compute the work done on this particle by the force field .
SolutionLet with and .
By Green’s theorem,
Let and let be the curve that is the top half of the circle , traversed counterclockwise from to , and the line segment from to . Evaluate the line integral
SolutionWe consider the integrals over the semicircle, denoted by , and the line segment, denoted by , seperately. We then have,
For the semicircle, we use the parametric equations
This yields
For the line segment, we use the parametric equations
This yields
We conclude
In evaluating these integrals, we have taken advantage of the rule,