Tutorial 9

Tutorial 9: Application of integral

Tutorial QuestionTutorial Solution

1. Find the area bounded by the curves.

   i. $y=x^{4}-x^{2}$ and $y=x^{2}$ (the part to the right of the $y$-axis)

   Solution

   We first need to compute where the graphs of the functions intersect. Setting $f(x)=g(x)$, we get,

   $$\begin{aligned} f(x)&=g(x) \\ x^4-x^2&=x^2 \end{aligned}$$

   $x=0, \sqrt{2}$ (only positive at the right side)

   $$\begin{aligned} A&=\int_0^{\sqrt{2}} f(x) d x-\int_0^{\sqrt{2}} g(x) d x \\ &=\int_0^{\sqrt{2}}\left(x^4-x^2-x^2\right) d x \\ &=-2-\left(\frac{2^{\frac{5}{2}}}{5}-2 \cdot \frac{2^{\frac{3}{2}}}{3}\right) \\ &=\frac{2^{7 / 2}}{15}-2 \end{aligned}$$

   ii. $x=y^{3}$ and $x=y^{2}$

   Solution

   We first need to compute where the graphs of the functions intersect. Setting $f(x)=g(x)$, we get,

   $$\begin{aligned} f(y)&=g(y) \\ y^3&=y^2 \\ y&=1,0 \end{aligned}$$

   Now,

   $$\begin{aligned} A&=\int_0^1 f(y) d y-\int_0^1 g(y) d y \\ &=\int_0^1\left(y^3-y^2\right) d y=\frac{1}{12} \end{aligned}$$

   iii. $y=\cos (\pi x / 2)$ and $y=1-x^{2}$ (in the first quadrant)

   Solution

   As from the Figure, we can see intersect of the two lines is $(-1, 1)$. Since we only compute the first quadrant, the limit will be $(0, 1)$.

   

   Now we get,

   $$\begin{aligned} \mathrm{A} &=\int_0^1 f(x) d x-\int_0^1 g(x) d x \\ &=\int_0^1\left(1-x^2-\cos \frac{\pi x}{2}\right) d x \\ &=\left|x-\frac{x^3}{3}-\frac{2}{\pi} \sin \frac{\pi x}{2}\right|_0^1 \\ &=\frac{2}{3}-\frac{2}{\pi} \approx 0.03 \text { Unit } \end{aligned}$$

2. Find the area bounded by the parabola $x=8+2 y-y^{2}$, the $y$-axis, and the lines $y=-1$ and $y=3$.

   Solution

   $$\begin{aligned} x & =8+2y-y^{2}\\ & =-\left( y^{2} -2y-8\right)\\ & =-\left(( y-1)^{2} -9\right)\\ & =( 4-y)( 2+y) \end{aligned}$$

   $\therefore$ The vortex of the parabola is $(9,1)$ and cuts the y-axis at $y=-4$, $y=-2$.

   Area bounded by the parabola:

   $$\begin{aligned} \int _{-1}^{3}\left( 8+2y-y^{2}\right) \ dy & =\left. 8y+y^{2} -\frac{1}{3} y^{3}\right| _{-1}^{3}\\ & =\left( 8( 3) +3^{2} -\frac{1}{3}( 3)^{3}\right) -\left( 8( -1) +( -1)^{2} -\frac{1}{3}( -1)^{3}\right)\\ & =\frac{92}{3} \end{aligned}$$

3. Assume a cylindrical tank of radius $4 \mathrm{~m}$ and height $10 \mathrm{~m}$ is filled to a depth of $8 \mathrm{~m}$ as shown Figure 3.1. How much work is needed to empty a tank partially filled with water?

   

   Figure 3.1 A tank partially filled with water

   Solution

   The first thing we need to do is define a frame of reference. We let $x$ represent the vertical distance below the top of the tank. That is, we orient the $x$-axis vertically, with the origin at the top of the tank and the downward direction being positive (Figure 3.1).

   Using this coordinate system, the water extends from $x=2$ to $x=10$ . Therefore, we partition the interval $[2,10]$ and look at the work required to lift each individual "layer" of water. So, for $i=0,1,2,\ldots,n$ , let $P=x_i$ be a regular partition of the interval $[2,10]$, and for $i=1,2,\ldots,n$ , choose an arbitrary point $x\times i\in[x_i-1,x_i]$. Figure 3.2 shows a representative layer.

   

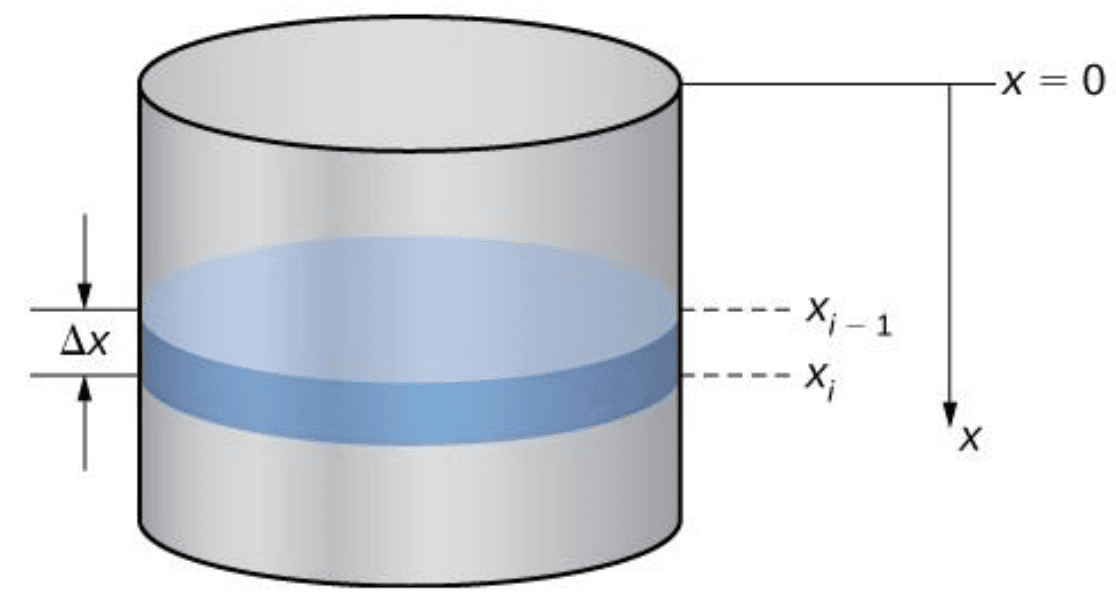
   In pumping problems, the force required to lift the water to the top of the tank is the force required to overcome gravity, so it is equal to the weight of the water. Given that the weight-density of water is $9800 \text{N/m}^3$, or $62.4\text{lb/ft}^3$, calculating the volume of each layer gives us the weight. In this case, we have:

   $$V=\pi(4)^2\Delta x=16\pi\Delta x$$

   Then, the force needed to lift each layer is,

   $$F=9800\cdot 16\pi\Delta x=156,800\pi\Delta x$$

   Note that this step becomes a little more difficult if we have a noncylindrical tank. We look at a noncylindrical tank in the next example.

   We also need to know the distance the water must be lifted. Based on our choice of coordinate systems, we can use $x_i^*$ as an approximation of the distance the layer must be lifted. Then the work to lift the $i$-th layer of water $W_i$ is approximately:

   $$W_i\approx156,800\pi x_i^*\Delta x$$

   Adding the work for each layer, we see the approximate work to empty the tank is given by

   $$W=\sum_{i=1}^n W_i\approx\sum_{i=1}^n 156,800\pi x_i^*\Delta x$$

   This is a Riemann sum, so taking the limit as $n\rightarrow\infty$, we get,

   $$\begin{aligned} W&=\lim_{n\rightarrow\infty}\sum_{i=1}^n 156,800\pi x_i^* \Delta x\\ &=156,800\pi\int_2^{10} x dx\\ &=\left.156,800\pi\left(\frac{x^2}{2}\right)\right|_2^{10}\\ &=7,526,400\pi\approx23,644,883 \end{aligned}$$

   The work required to empty the tank is approximately 23,650,000 J.

4. An object moves along a straight line with acceleration given by $a(t)=-\cos (t)$, and $s(0)=1$ and $v(0)=0$. Find the maximum distance the object travels from zero, and find its maximum speed. Describe the motion of the object.

   Solution

   We compute:

   $$\begin{aligned} v(t)&=v_0+\int_0^t-\cos(u)du\\ &=\left.0-\sin(u)\right|_0^t\\ &=-\sin t \end{aligned}$$

   The maximum distance travelled is then:

   $$s=\int v(t)dt=\int-\sin t dt=\cos t$$

5. A particle at rest leaves the origin with its velocity increasing with time according to $\mathrm{v}(\mathrm{t})=3.2 \mathrm{t} \mathrm{m} / \mathrm{s}$. At $5.0 \mathrm{~s}$, the particle's velocity starts decreasing according to $[16.0-1.5(\mathrm{t}-5.0)] \mathrm{m} / \mathrm{s}$. This decrease continues until $\mathrm{t}=11.0 \mathrm{~s}$, after which the particle's velocity remains constant at $7.0 \mathrm{~m} / \mathrm{s}$. (a) What is the acceleration of the particle as a function of time? (b) What is the position of the particle at $\mathrm{t}=2.0 \mathrm{~s}, \mathrm{t}=7.0 \mathrm{~s}$, and $\mathrm{t}=12.0 \mathrm{~s}$ ?

   Solution

   (a)

   $$\begin{aligned} a(t)&=3.2 \mathrm{~m} / \mathrm{s}^2 && t\leq 5.0 \mathrm{~s}\\ a(t)&=1.5 \mathrm{~m} / \mathrm{s}^2 && 5.0 \mathrm{~s} \leq t \leq 11.0 \mathrm{~s}\\ a(t)&=0 \mathrm{~m} / \mathrm{s}^2 && t>11.0 \mathrm{~s}\\ x(t)&=\int v(t) d t+C_2\\ &=\int 3.2 t d t+C_2=1.6 t^2+C_2 && t \leq 5.0 \mathrm{~s}\\ x(0)&=0 \Rightarrow C_2=0 && \text{therefore, } x(2.0 \mathrm{~s})=6.4 \mathrm{~m}\\ x(t)&=\int v(t) d t+C_2\\ &=\int[16.0-1.5(t-5.0)] d t+C_2\\ &=16 t-1.5\left(\frac{t^2}{2}-5.0 t\right)+C_2 &&5.0 \leq t \leq 11.0 \mathrm{~s}\\ x(5 \mathrm{~s})&=1.6(5.0)^2=40\mathrm{~m}\\ &=16(5.0 \mathrm{~s})-1.5\left(\frac{5^2}{2}-5.0(5.0)\right)+C_2 \end{aligned}$$

   (b)

   $$\begin{aligned} 40&=98.75+C_2 \Rightarrow C_2=-58.75\\ x(7.0 \mathrm{~s})&=16(7.0)-1.5\left(\frac{7^2}{2}-5.0(7)\right)-58.75=69 \mathrm{~m}\\ x(t)&=\int 7.0 d t+C_2=7 t+C_2 \qquad t \geq 11.0 \mathrm{~s}\\ x(11.0 \mathrm{~s})&=16(11)-1.5\left(\frac{11^2}{2}-5.0(11)\right)-58.75=109=7(11.0 \mathrm{~s})+C_2 \Rightarrow C_2=32 \mathrm{~m}\\ x(t)&=7 t+32 \mathrm{~m}\\ x &\geq 11.0 \mathrm{~s} \Rightarrow x(12.0 \mathrm{~s})=7(12)+32=116 \mathrm{~m} \end{aligned}$$

6. A force of $50 \mathrm{~N}$ will stretch a spring from its natural length of 2 meters to a length of $2.5$ meters.

   i. Find the spring constant.

   Solution

   we find that the spring constant $k$ is,

   $$\begin{aligned} k(0.5 \mathrm{~m}) &= 50 \mathrm{~N}\\ k &= 100 \text{N/m} \end{aligned}$$

   ii. Find the work needed to stretch the spring by a length of $0.5$ meter from its natural length.

   Solution

   By Hooke’s Law, the force needed to compress the spring by a length of $x$ feet from its natural length is

   $$f(x) = kx = 100x$$

   since $k = 100$.

   As the spring expand from a length of 2m to a length of 2.5m, we can think of one end of the spring as moving along the x-axis from $x = 0$ to $x = 0.5$ while the other end of the spring is held fixed. Then the work done is,

   $$W=\int_0^{0.5}100xdx=100\cdot\frac{0.5^2}{2}=0.25\text{ Joule}$$

7. Find the arc length $L$ of the curve $y=x 3 / 2$ from $x=0$ to $x=5$.

   Solution

   $$y' =\frac{3}{2} x^{\frac{1}{2}} =\frac{3}{2}\sqrt{x}$$

   $$\begin{aligned} L & =\int _{0}^{5}\sqrt{1+( y')^{2}} \ dx\\ & =\int _{0}^{5}\sqrt{1+\left(\frac{3}{2}\sqrt{x}\right)^{2}} \ dx\\ & =\int _{0}^{5}\sqrt{1+\frac{9}{4} x} \ dx\\ & =\int _{0}^{5}\left( 1+\frac{9}{4} x\right)^{\frac{1}{2}} \ dx\\ & =\left. \frac{\left( 1+\frac{9}{4} x\right)^{\frac{3}{2}}}{\left(\frac{3}{2}\right)\left(\frac{9}{4}\right)}\right| _{0}^{5}\\ & =\frac{\left( 1+\frac{9}{4}( 5)\right)^{\frac{3}{2}}}{\frac{27}{8}} -\frac{\left( 1+\frac{9}{4}( 0)\right)^{\frac{3}{2}}}{\frac{27}{8}}\\ & =\frac{335}{27} \end{aligned}$$

8. Find the arc length of the catenary $\displaystyle y=\frac{a}{2}\left(e^{\frac{x}{a}}+e^{\frac{-x}{a}}\right)$ from $x=0$ to $x=a$.

   Solution

   $$\begin{aligned} y' & =\frac{a}{2}\left(\frac{1}{a} e^{\frac{x}{a}} -\frac{1}{a} e^{-\frac{x}{a}}\right) +0\left( e^{\frac{x}{a}} +e^{-\frac{x}{a}}\right)\\ & =\frac{a}{2}\left(\frac{1}{a}\right)\left( e^{\frac{x}{a}} -e^{-\frac{x}{a}}\right)\\ & =\frac{1}{2}\left( e^{\frac{x}{a}} -e^{-\frac{x}{a}}\right) \end{aligned}$$

   Arc length:

   $$\begin{aligned} L & =\int _{0}^{a}\sqrt{1+( y')^{2}} \ dx\\ & =\int _{0}^{a}\sqrt{1+\left[\frac{1}{2}\left( e^{\frac{x}{a}} -e^{-\frac{x}{a}}\right)\right]^{2}} dx\\ & =\int _{0}^{a}\sqrt{1+\frac{1}{4}\left( e^{\frac{2x}{a}} -2e^{0} +e^{-\frac{2x}{a}}\right)} dx\\ & =\int _{0}^{a}\sqrt{1+\frac{1}{4} e^{\frac{2x}{a}} -\frac{1}{2} +\frac{1}{4} e^{-\frac{2x}{a}}} dx\\ & =\int _{0}^{a}\sqrt{\frac{1}{4} e^{\frac{2x}{a}} +\frac{1}{2} +\frac{1}{4} e^{-\frac{2x}{a}}} dx\\ & =\int _{0}^{a}\sqrt{\frac{1}{4}\left[ e^{\frac{2x}{a}} +2+ e^{-\frac{2x}{a}}\right]} dx\\ & =\int _{0}^{a}\sqrt{\frac{1}{4}\left( e^{\frac{x}{a}} +e^{-\frac{x}{a}}\right)^{2}} dx\\ & =\int _{0}^{a}\frac{1}{2}\left( e^{\frac{x}{a}} +e^{-\frac{x}{a}}\right) \ dx\\ & =\frac{1}{2}\int _{0}^{a}\left( e^{\frac{x}{a}} +e^{-\frac{x}{a}}\right) \ dx\\ & =\frac{1}{2}\left[\left. \frac{e^{\frac{x}{a}}}{\frac{1}{a}} -\frac{e^{-\frac{x}{a}}}{\frac{1}{a}}\right| _{0}^{a}\right]\\ & =\frac{1}{2} \div a\left[ e^{1} +e^{-1} -1+1\right]\\ & =\frac{a}{2}\left[ e-e^{-1}\right] \end{aligned}$$

9. Find the centroid of the plane area bounded by the parabolas $y=2 x-x^{2}$ and $y=3 x^{2}-6 x$

   Solution

   

   $$\begin{aligned} A & =\int \int\limits _{R} dA\\ & =\int _{0}^{2}\int _{3x^{2} -6x}^{2x-x^{2}} dydx\\ & =\int _{0}^{2}\left[ 2x-x^{2} -3x^{2} +6x\right] dx\\ & =\int _{0}^{2}\left[ -4x^{2} +8x\right] dx\\ & =\left. \frac{-4x^{3}}{3} +4x^{2}\right| _{0}^{2}\\ & =\frac{-4( 2)^{3}}{3} +4( 2)^{2}\\ & =\mathbf{\frac{16}{3}} \end{aligned}$$

   $$\begin{aligned} M_{y} & =\int \int\limits _{R} x\ dA\\ & =\int _{0}^{2}\int _{3x^{2} -6x}^{2x-x^{2}} x\ dydx\\ & =\int _{0}^{2} x\left( 2x-x^{2} -3x^{2} +6x\right) \ dx\\ & =\int _{0}^{2}\left[ -4x^{3} +8x^{2}\right] dx\\ & =\left. -x^{4} +\frac{8}{3} x^{3}\right| _{0}^{2}\\ & =-2^{4} +\frac{8}{3}( 2)^{3}\\ & =\mathbf{\frac{16}{3}} \end{aligned}$$

   $$\begin{aligned} M_{x} & =\int \int\limits _{R} y\ dA\\ & =\int _{0}^{2}\int _{3x^{2} -6x}^{2x-x^{2}} y\ dydx\\ & =\frac{1}{2}\int _{0}^{2}\left[\left( 2x-x^{2}\right)^{2} -\left( 3x^{2} -6x\right)^{2}\right] dx\\ & =\frac{1}{2}\int _{0}^{2}\left[ 4x^{2} -4x^{3} +x^{4} -9x^{4} +36x^{3} -36x^{2}\right] dx\\ & =\frac{1}{2}\int _{0}^{2}\left[ -8x^{4} +32x^{3} -32x^{2}\right] dx\\ & =\frac{1}{2}\left[\left. -\frac{8}{5} x^{5} +8x^{4} -\frac{32}{3} x^{3}\right| _{0}^{2}\right]\\ & =\frac{1}{2}\left[ -\frac{8}{5}( 2)^{5} +8( 2)^{4} -\frac{32}{3}( 2)^{3}\right]\\ & =-\frac{64}{15} \end{aligned}$$

   Hence, $x=\frac{M_{y}}{A} =\frac{\frac{16}{3}}{\frac{16}{3}} =1$, $y=\frac{M_{x}}{A} =\frac{-\frac{64}{15}}{\frac{16}{3}} =-\frac{4}{5}$. Thus, the centroid is $\left( 1,-\frac{4}{5}\right)$.

10. Find the hydrostatic force on a circular plate of radius 2 that is submerged 6 meters in the water.

    Solution

    

    Assume that the top of the circular plate is 6 meters under the water.

    Setting up the axis system such that the origin of the axis is at the center of the plate.

    Finally, split up the plate into $n$ horizontal strips each of width $\Delta y$. Choosing a point $y_{i}^{*}$ from each strip. Assume that the strips are rectangular.

    The depth below the water surface of each strip is,

    $$d_{i} =8-y_{i}^{*}$$

    and that in turn gives us the pressure on the strip,

    $$P_{i} =\rho gd_{i} =9810\left( 8-y_{i}^{*}\right)$$

    The area of each strip is,

    $$A_{i} =2\sqrt{4-\left( y_{i}^{*}\right)^{2}} \ \ \Delta y$$

    The hydrostatic force on each strip is,

    $$F_{i} =P_{i} A_{i} =9810\left( 8-y_{i}^{*}\right)( 2)\sqrt{4-\left( y_{i}^{*}\right)^{2}} \ \ \Delta y$$

    The total force on the plate is,

    $$\begin{aligned} F & =\lim\limits _{n\rightarrow \infty }\sum\limits _{i=1}^{n} 19620\left( 8-y_{i}^{*}\right)\sqrt{4-\left( y_{i}^{*}\right)^{2}} \ \ \Delta y\\ & =19620\int _{\ -2}^{\ 2}( 8-y)\sqrt{4-y^{2}} \ dy\\ & =19620\int _{\ -2}^{\ 2} 8\sqrt{4-y^{2}} \ dy-19620\int _{\ -2}^{\ 2} y\sqrt{4-y^{2}} \ dy \end{aligned}$$

    The first integral requires the trig substitution $y=2\sin \theta$ and the second integral needs the substitution $v=4-y^{2}$.

    $$\begin{aligned} F & =627840\int _{\ -\pi /2\ }^{\ \pi /2\ }\cos^{2} \theta \ d\theta +9810\int _{\ 0}^{\ 0}\sqrt{v} \ dv\\ & =313920\int _{\ -\pi /2\ }^{\ \pi /2\ } 1+\cos( 2\theta ) \ d\theta +0\\ & =313920\left. \left( \theta +\frac{1}{2}\sin( 2\theta )\right)\right| _{-\pi /2}^{\pi /2}\\ & =313920\pi \end{aligned}$$

Your Help needed

This website has received 3000 view in the first two weeks! However, this project repository did not receive any star! Just simply head over to this website's repository to give it a star! Every tutorial takes me around two hours to compile, proof-read and styling this website! Your simple action would encourage me a lot! Thank you! You could Buy me a coffee too!