Tutorial 2

Tutorial 2: Partial Derivatives Engineering Applications of Partial Derivatives

Tutorial QuestionTutorial Solution

1. Find the partial derivative $\displaystyle\left(\frac{\partial f}{\partial y}\right)$ and $\displaystyle\left(\frac{\partial f}{\partial x}\right)$ of these functions using the limit definition

   a. $f(x, y)=x^{2} y+2 x+y^{3}$

   Solution

   $$\begin{aligned} f_{x}(x, y) &=\lim _{h \rightarrow 0} \frac{f(x+h, y)-f(x, y)}{h} \\ &=\lim _{h \rightarrow 0} \frac{(x+h)^{2} y+2(x+h)+y^{3}-\left(x^{2} y+2 x+y^{3}\right)}{h} \\ &=\lim _{h \rightarrow 0} \frac{x^{2} y+2 x h y+h^{2} y+2 x+2 h+y^{3}-\left(x^{2} y+2 x+y^{3}\right)}{h} \\ &=\lim _{h \rightarrow 0} \frac{2 x h y+h^{2} y+2 h}{h} \\ &=\lim _{h \rightarrow 0} 2 x y+h y+2 \\ &=2 x y+2 \\ f_{y}(x, y) &=\lim _{h \rightarrow 0} \frac{f(x, y+h)-f(x, y)}{h} \\ &=\lim _{h \rightarrow 0} \frac{x^{2}(y+h)+2 x+(y+h)^{3}-x^{2} y-2 x-y^{3}}{h} \\ &=\lim _{h \rightarrow 0} \frac{x^{2} y+x^{2} h+2 x+y^{3}+3 y^{2} h+3 y h^{2}+h^{3}-x^{2} y-2 x-y^{3}}{h} \\ &=\lim _{h \rightarrow 0} \frac{x^{2} h+3 y^{2} h+3 y h^{2}+h^{3}}{h} \\ &=\lim _{h \rightarrow 0} x^{2}+3 y^{2}+3 y h+h^{2} \\ &=x^{2}+3 y^{2} \end{aligned}$$

   b. $f(x, y)=x^{2}-4 x y+y^{2}$

   Solution

   Using the definition,

   $$\begin{aligned} f_{x}(x, y) &=\lim _{h \rightarrow 0} \frac{f(x+h, y)-f(x, y)}{h} \\ &=\lim _{h \rightarrow 0} \frac{(x+h)^{2}-4(x+h) y+y^{2}-\left(x^{2}-4 x y+y^{2}\right)}{h} \\ &=\lim _{h \rightarrow 0} \frac{x^{2}+2 x h+h^{2}-4 x y-4 h y+y^{2}-\left(x^{2}-4 x y+y^{2}\right)}{h} \\ &=\lim _{h \rightarrow 0} \frac{2 x h+h^{2}-4 h y}{h} \\ &=\lim _{h \rightarrow 0}(2 x+h-4 y) \\ &=2 x-4 y \end{aligned}$$

   Similarly,

   $$\begin{aligned} f_{y}(x, y) &=\lim _{h \rightarrow 0} \frac{f(x, y+h)-f(x, y)}{h} \\ &=\lim _{h \rightarrow 0} \frac{x^{2}-4 x(y+h)+(y+h)^{2}-\left(x^{2}-4 x y+y^{2}\right)}{h} \\ &=\lim _{h \rightarrow 0} \frac{x^{2}-4 x y-4 x h+y^{2}+2 y h+h^{2}-\left(x^{2}-4 x y+y^{2}\right)}{h} \\ &=\lim _{h \rightarrow 0} \frac{-4 x h+2 y h+h^{2}}{h} \\ &=\lim _{h \rightarrow 0}(-4 x+2 y+h) \\ &=-4 x+2 y \end{aligned}$$

   c. $f(x, y)=2 x^{3}+3 x y-y^{2}$

   Solution

   $$\begin{aligned} \frac{\partial f}{\partial x} &= \lim _{h \rightarrow 0} \frac{f(x+h, y)-f(x, y)}{h} \\ &=\lim _{h \rightarrow 0} \frac{h\left(6 x^{2}+6 x h+2 h^{2}+3 y\right)}{h} \\ &=\lim _{h \rightarrow 0}\left(6 x^{2}+6 x h+2 h^{2}+3 y\right) \\ &=6 x^{2}+3 y \\ \frac{\partial f}{\partial y} &= \lim _{h \rightarrow 0} \frac{f(x, y+h)-f(x, y)}{h} \\ &=\lim _{h \rightarrow 0} \frac{h(3 x-2 y-h)}{h} \\ &=\lim _{h \rightarrow 0}(3 x-2 y-h) \\ &=3 x-2 y \end{aligned}$$

2. Determine all the first and second order partial derivatives of the function

   a. $f(x, y)=x^{2} y^{3}+3 y+x$

   Solution

   $$\begin{aligned} \frac{\partial f}{\partial x}&= 2xy^3+1 \\ \frac{\partial f}{\partial y}&= 3x^2y^2+3 \\ \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)&= 2y^3 \\ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)&= 6xy^2 \\ \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)&= 6xy^2 \\ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)&= 6x^2y \\ \end{aligned}$$

   b. $f(x, y)=x^{4} \sin 3 y$

   Solution

   $$\begin{aligned} \frac{\partial f}{\partial x}&= 4x^3\sin{3y} \\ \frac{\partial f}{\partial y}&= 3x^4\cos{3y} \\ \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)&= 12x^2\sin{3y} \\ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)&= 12x^3\cos{3y} \\ \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)&= 12x^3\cos{3y} \\ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)&= -9x^4\sin{3y} \\ \end{aligned}$$

   c. $f(x, y)=x^{2} y+\ln \left(y^{2}-x\right)$

   Solution

   $$\begin{aligned} \frac{\partial f}{\partial x}&= 2xy-\frac{1}{y^2-x} \\ \frac{\partial f}{\partial y}&= x^2+\frac{2y}{y^2-x} \\ \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)&= 2y-\frac{1}{(y^2-x)^2} \\ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)&= 2x+\frac{2y}{(y^2-x)^2} \\ \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)&= 2x+\frac{2y}{(y^2-x)^2} \\ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)&= \frac{-2y^2-2x}{(y^2-x)^2} \\ \end{aligned}$$

   d. $f(x, y)=e^{x y}(2 x-y)$

   Solution

   $$\begin{aligned} \frac{\partial f}{\partial x}&= e^{xy}(2xy-y^2+2) \\ \frac{\partial f}{\partial y}&= e^{xy}(2x^2-xy-1) \\ \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)&= e^{xy}(2xy^2-y^3+4y) \\ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)&= e^{xy}(2x^3y-xy^2+4x-2y) \\ \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)&= e^{xy}(2x^2y-xy^2+4x-2y) \\ \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)&= e^{xy}(2x^3-x^2y-2x)\\ \end{aligned}$$

3. Find both partial derivatives for each of the following two variables functions

   a. $g(x, y)=y e^{x+y}$

   Solution

   $$\begin{aligned} g(x, y)=& y e^{x+y} \\ g_{x}(x, y) &=y e^{x+y} \\ g_{y}(x, y) &=e^{x+y}+y e^{x+y} \end{aligned}$$

   b. $h(x, y)=x \sin y-y \cos x$

   Solution

   $$\begin{aligned} &h(x, y)=x \sin y-y \cos x \\ &h_{x}(x, y)=\sin y+y \sin x \\ &h_{y}(x, y)=x \cos y-\cos x \end{aligned}$$

   c. $p(x, y)=x^{y}+y^{2}$

   Solution

   $$\begin{aligned} p(x, y)=& x^{y}+y^{2} \\ p_{x}(x, y) &=y x^{y-1} \\ p_{y}(x, y) &=x^{y} \ln x+2 y \end{aligned}$$

   d. $U(x, y)=\frac{9 y^{3}}{x-y}$

   Solution

   $$\begin{aligned} &\frac{\partial U}{\partial x}=U_{x}=\frac{(x-y)(0)-9 y^{3}(1)}{(x-y)^{2}}=\frac{-9 y^{3}}{(x-y)^{2}} \\ &\frac{\partial U}{\partial y}=U_{y}=\frac{(x-y)\left(27 y^{2}\right)-9 y^{3}(-1)}{(x-y)^{2}}=\frac{27 x y^{2}-18 y^{3}}{(x-y)^{2}} \end{aligned}$$

4. For $f(x, y, z)$, use the implicit function theorem to find $d y / d x$ and $d y / d z$

   a. $f(x, y, z)=x^{2} y^{3}+z^{2}+x y z$

   Solution

   $$\begin{gathered} f(x, y, z)=x^{2} y^{3}+z^{2}+x y z \\ \frac{d y}{d x}=-\frac{f x}{f y}=-\frac{2 x y^{3}+y z}{3 x^{2} y^{2}+x z} \\ \frac{d y}{d z}=-\frac{f z}{f y}=-\frac{2 z+x y}{3 x^{2} y^{2}+x z} \end{gathered}$$

   b. $f(x, y, z)=x^{3} z^{2}+y^{3}+4 x y z$

   Solution

   $$\begin{gathered} f(x, y, z)=x^{3} z^{2}+y^{3}+4 x y z \\ \frac{d y}{d x}=-\frac{f x}{f y}=-\frac{3 x^{2} z^{2}+4 y z}{3 y^{2}+4 x z} \\ \frac{d y}{d z}=-\frac{f z}{f y}=-\frac{2 x^{3} z+4 x y}{3 y^{2}+4 x z} \end{gathered}$$

   c. $f(x, y, z)=3 x^{2} y^{3}+x z^{2} y^{2}+y^{3} z x^{4}+y^{2} z$

   Solution

   $$\begin{gathered} f(x, y, z)=3 x^{2} y^{3}+x z^{2} y^{2}+y^{3} z x^{4}+y^{2} z \\ \frac{d y}{d x}=-\frac{f x}{f y}=-\frac{6 x y^{3}+z^{2} y^{2}+4 y^{3} z x^{3}}{9 x^{2} y^{2}+2 x z^{2} y+3 y^{2} z x^{4}+2 y z} \\ \frac{d y}{d z}=-\frac{f z}{f y}=-\frac{2 x z y^{2}+y^{3} x^{4}+y^{2}}{9 x^{2} y^{2}+2 x z^{2} y+3 y^{2} z x^{4}+2 y z} \end{gathered}$$

5. Find $\frac{\partial F}{\partial s}$ and $\frac{\partial F}{\partial t}$, if applicable, for the following composite functions

   a. $F=\sin (x+y)$ where $x=2st$ and $y=s^2+t^2$

   Solution

   $$\begin{aligned} \frac{\partial F}{\partial s}&=\frac{\partial F}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial F}{\partial y} \frac{\partial y}{\partial s} \\ &=\cos (x+y)(2t)+\cos (x+y)(2s) \\ &=2t\cos (2st+s^2+t^2)+2s\cos (st+s^2+t^2) \\ &= 2\cos ((s+t)^2)(s+t) \end{aligned}$$

   $$\begin{aligned} \frac{\partial F}{\partial t}&=\frac{\partial F}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial F}{\partial y} \frac{\partial y}{\partial t} \\ &=\cos (x+y)(2s)+\cos (x+y)(2t) \\ &= 2\cos ((s+t)^2)(s+t) \end{aligned}$$

   b. $F=\ln \left(x^{2}+y\right)$ where $x=\mathrm{e}^{(s+t 2)}$ and $y=s^{2}+t$

   Solution

   $$\begin{aligned} \frac{\partial F}{\partial s} & =\frac{\partial F}{\partial x}\frac{\partial x}{\partial s} +\frac{\partial F}{\partial y}\frac{\partial y}{\partial s}\\ & =\frac{2x}{x^{2} +y} e^{s+t^{2}} +\frac{1}{x^{2} +y} 2s\\ & =\frac{2}{x^{2} +y}\left( xe^{s+t^{2}} +s\right) \end{aligned}$$

   $$\begin{aligned} \frac{\partial F}{\partial t} & =\frac{\partial F}{\partial x}\frac{\partial x}{\partial t} +\frac{\partial F}{\partial y}\frac{\partial y}{\partial t}\\ & =\frac{2x}{x^{2} +y} 2te^{s+t^{2}} +\frac{1}{x^{2} +y}( 1)\\ & =\frac{1}{x^{2} +y}\left( 4xte^{s+t^{2}} +1\right) \end{aligned}$$

   c. $F=x^{2} y^{2}$ where $x=s \cos t$ and $y=s \sin t$

   Solution

   $$\begin{aligned} \frac{\partial F}{\partial s} & =\frac{\partial F}{\partial x}\frac{\partial x}{\partial s} +\frac{\partial F}{\partial y}\frac{\partial y}{\partial s}\\ & =2xy^{2}\cos t+2x^{2} y\sin t\\ & =2( s\cos t)\left( s^{2}\sin^{2} t\right)(\cos t) +2\left( s^{2}\cos^{2} t\right)( s\sin t)(\sin t)\\ & =2s^{3}\cos^{2} t\sin^{2} t+2s^{3}\cos^{2} t\sin^{2} t\\ & =4s^{3}\cos^{2} t\sin^{2} t\\ & =4s^{3}(\cos t\sin t)^{2}\\ & =4s^{3}\left(\frac{1}{2}\sin 2t\right)^{2}\\ & =s^{3}(\sin 2t)^{2} \end{aligned}$$

   $$\begin{aligned} \frac{\partial F}{\partial t} & =\frac{\partial F}{\partial x}\frac{\partial x}{\partial t} +\frac{\partial F}{\partial y}\frac{\partial y}{\partial t}\\ & =2xy^{2}( -s\sin t) +2x^{2} y( s\cos t)\\ & =2x^{2} ys\cos t-2xy^{2} s\sin t\\ & =2\left( s^{2}\cos^{2} t\right)( s\sin t) s\cos t-2( s\cos t)\left( s^{2}\sin^{2} t\right) s\sin t\\ & =2s^{4}\cos^{3} t\sin t-2s^{4}\cos t\sin^{3} t\\ & =2s^{4}(\cos t\sin t)\left(\cos^{2} t-\sin^{2} t\right)\\ & =2s^{4}\left(\frac{1}{2}\sin 2t\right)(\cos 2t)\\ & =s^{4}\sin 2t\cos 2t \end{aligned}$$

   d. $F=xy+y \mathrm{z}^{2}$ where $x=\mathrm{e}^{t}, y=\mathrm{e}^{t} \sin t$ and $\mathrm{z}=\mathrm{e}^{t} \cos t$

   Solution

   $$\begin{aligned} \frac{dF}{dt} & =\frac{\partial F}{\partial x}\frac{\partial x}{\partial t} +\frac{\partial F}{\partial y}\frac{\partial y}{\partial t} +\frac{\partial F}{\partial z}\frac{\partial z}{\partial t}\\ & =ye^{t} +\left( x+z^{2}\right)\left( e^{t}\cos t+\sin^{t} e^{t}\right) +2yz\left( -e^{t}\sin t+\cos te^{t}\right)\\ & =ye^{t} +xe^{t}\cos t+x\sin^{t} e^{t} +z^{2} e^{t}\cos t+z^{2}\sin te^{t} -2yze^{t}\sin t+2yz\cos te^{t}\\ & =ye^{t} +e^{t}\cos t\left( x+z^{2} +2yz\right) +e^{t}\sin t\left( x+z^{2} -2yz\right)\\ & =e^{t}\sin t\cdot e^{t} +e^{t}\cos t\left( e^{t} +e^{2t}\cos t+2e^{2t}\sin t\cos t\right)\\ & \ \ \ \ \ +e^{t}\sin t\left( e^{t} +e^{2t}\cos^{2} t-2e^{2t}\sin t\cos t\right)\\ & =e^{2t}\sin t+e^{2t}\cos t+e^{3t}\cos^{3} t+2e^{2t}\sin t\cos^{2} t+e^{2t}\sin t+e^{3t}\sin t\cos^{2} t\\ & \ \ \ \ \ -2e^{3} t\sin^{2} t\cos t\\ & =2e^{2t}\sin t+e^{2t}\cos t+e^{3t}\cos^{3} t+3e^{3t}\sin t\cos^{2} t-2e^{3t}\sin^{2} t\cos t\\ & =e^{2t}( 2\sin t+\cos t) +e^{3t}\left(\cos^{3} t+3\sin t\cos^{2} t-2\sin^{2} t\cos t\right) \end{aligned}$$

6. Find $d y / d x$ and $d y / d z$ (if applicable) for each of the following

   a. $7 x^{2}+2 x y^{2}+9 y^{4}=0$

   Solution

   $$\begin{aligned} \frac{dy}{dx} & =-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} =-\frac{14x+2y^{2}}{36y^{2} +4xy} \end{aligned}$$

   b. $x^{3} z^{2}+y^{3}+4 x y z=0$

   Solution

   $$\begin{aligned} \frac{dy}{dx} & =-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} =-\frac{3x^{2} z^{2} +4yz}{3y^{2} +4xz}\\ \frac{dy}{dz} & =-\frac{\frac{\partial F}{\partial z}}{\frac{\partial F}{\partial y}} =-\frac{2x^{3} z+4xy}{3y^{2} +4xz} \end{aligned}$$

   c. $3 x^{2} y^{3}+x z^{2} y^{2}+y^{3} z x^{4}+y^{2} z=0$

   Solution

   $$\begin{aligned} \frac{dy}{dx} & =-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} =-\frac{6xy^{3} +z^{2} y^{2} +4y^{3} zx^{3}}{9x^{2} y^{2} +2xz^{2} y+3y^{2} zx^{4} +2yz}\\ \frac{dy}{dz} & =-\frac{\frac{\partial F}{\partial z}}{\frac{\partial F}{\partial y}} =-\frac{2xzy^{2} +y^{3} x^{4} +y^{2}}{9x^{2} y^{2} +2xz^{2} y+3y^{z} x^{4} +2yz} \end{aligned}$$

   d. $y^{5}+x^{2} y^{3}=1+y \exp \left(x^{2}\right)$

   Solution

   $$\begin{aligned} \frac{dy}{dx} & =-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} =-\frac{2xy\left( y^{2} -e^{x^{2}}\right)}{5y^{4} +3x^{2} y^{2} -e^{x^{2}}} \end{aligned}$$

7. a. In polar coordinates, $x=r \cos \theta, y=r \sin \theta$, show that $\frac{\partial(x, y)}{\partial(r, \theta)}=r$

   Solution

   $$\begin{aligned} & \text { For } x=r \cos \theta, \frac{\partial x}{\partial r}=\cos \theta, \frac{\partial x}{\partial \theta}=-r \sin \theta \\ & y=r \sin \theta, \frac{\partial y}{\partial r}=\sin \theta, \frac{\partial y}{\partial \theta}=r \cos \theta \\ & \therefore \quad \frac{\partial(x, y)}{\partial(r, \theta)}=\left|\begin{array}{ll}\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta}\end{array}\right|=\left|\begin{array}{cc}\cos \theta & -r \sin \theta \\\sin \theta & r \cos \theta\end{array}\right|=r . \end{aligned}$$

   b. Obtain the Jacobian $J$ of the transformation $s=2 x+y, t=x-2 y$ and determine the inverse of the transformation $J_{1}$. Confirm that $J_{1}=J^{-1}$.

   Solution

   $$\begin{aligned} J & =\frac{\partial ( s,t)}{\partial ( x,y)}\\ & =\left| \begin{matrix} 2 & 1\\ 1 & -2 \end{matrix}\right| \\ & =-5 \end{aligned}$$

   $$\begin{array}{l} x=\frac{1}{5}( 2s+t) \quad \quad y=\frac{1}{5}( s-2t)\\ \\ \begin{aligned} J_{1} & =\frac{\partial ( x,y)}{\partial ( s,t)}\\ & =\left| \begin{matrix} \frac{2}{5} & \frac{1}{5}\\ \frac{1}{5} & -\frac{2}{5} \end{matrix}\right| \\ & =-\frac{1}{5} \end{aligned} \end{array}$$

   $$\therefore J_{1} =J^{-1}$$

   c. Show that if $x+y=\mathrm{u}$ and $y=\mathrm{uv}$, then $\frac{\partial(x, y)}{\partial(u, v)}=u$.

   Solution

   $$\begin{array}{l} x+uv=u\Longrightarrow x=u-uv\\ \frac{dx}{du} =1-v\\ \frac{dx}{dv} =-1 \end{array}$$

   $$\begin{array}{l} y=uv\\ \frac{dy}{du} =v\\ \frac{dy}{dv} =u \end{array}$$

   $$\begin{aligned} \frac{\partial ( x,y)}{\partial ( u,v)} & =\left| \begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u}\\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} \end{matrix}\right| \\ & =\left| \begin{matrix} 1-v & v\\ -u & u \end{matrix}\right| \\ & =u-uv+uv\\ & =u\ \end{aligned}$$

   d. Verify whether the functions $u=\frac{x+y}{1-x y}$ and $v=\tan ^{-1} x+\tan ^{-1} y$ are functionally dependent.

   Solution

   $$\begin{aligned} \frac{\partial ( u,v)}{\partial ( x,y)} & =\left| \begin{matrix} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{matrix}\right| =\left| \begin{matrix} \frac{1+y^{2}}{( 1-xy)^{2}} & \frac{1+x^{2}}{( 1-xy)^{2}}\\ \frac{1}{1+x^{2}} & \frac{1}{1+y^{2}} \end{matrix}\right| \\ & =\frac{1}{( 1-xy)^{2}} -\frac{1}{( 1-xy)^{2}}\\ & =0 \end{aligned}$$

   e. If $x=\mathrm{uv}, \frac{u+v}{u-v}$, find $\frac{\partial(u, v)}{\partial(x, y)}$.

   Solution

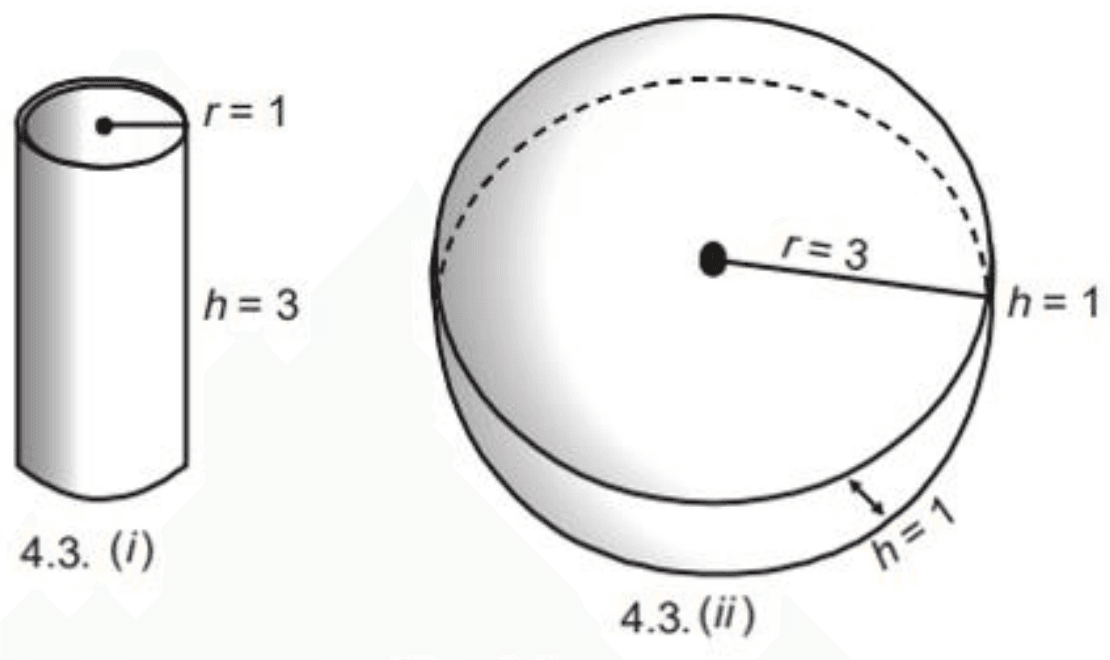
   $$\begin{aligned} \frac{\partial ( x,y)}{\partial ( u,v)} & =\left| \begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u}\\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} \end{matrix}\right| =\left| \begin{matrix} v & u\\ -\frac{2v}{( u-v)^{2}} & -\frac{2u}{( u-v)^{2}} \end{matrix}\right| \\ & =\frac{2uv}{( u-v)^{2}} +\frac{2uv}{( u-v)^{2}}\\ & =\frac{4uv}{( u-v)^{2}}\\ \frac{\partial ( u,v)}{\partial ( x,y)} & =\frac{( u-v)^{2}}{4uv} \end{aligned}$$

8. a. How sensitive is the volume $V=\pi r^{2} h$ of a right circular cylinder to small changes in its radius and height near the point $\left(r_{0}, h_{0}\right)=(1,3)$?

   Solution

   

   By increment method, we get

   $$\begin{aligned} \Delta V & \approx\left(\frac{\partial V}{\partial r}\right)_{\left(r_{0}, h_{0}\right)} \Delta r+\left(\frac{\partial V}{\partial h}\right)_{\left(r_{0}, h_{0}\right)} \Delta h \\ &=V_{r}(1,3) \Delta r+V_{h}(1,3) \Delta h \\ &=(2 \pi r h)_{(1,3)} \Delta r+\left(\pi r^{2}\right)_{(1,3)} \cdot \Delta h \\ &=6 \pi \cdot \Delta r+\pi \cdot \Delta h \end{aligned}$$

   The above result shows that a one-unit change in $r$ will change $V$ nearly by $\pi$ units and a one-unit change in $h$ will change $V$ nearly by $6 \pi$ units. Therefore, the volume of a cylinder with radius $r=1$ and height $h=3$ is nearly 6 times as sensitive to small change in $r$ as it is to small change in $h$ Fig. 4.3(i).

   In contrast, if value of $r$ and $h$ are reversed, so that $r=3$ and $h=1$, then $\Delta V \approx 6 \pi \cdot \Delta r+9 \pi$. $\Delta h$. The volume is now more sensitive to small change in $h$ to that it is to change in $r$. Thus the sensitivity to change depends not only on the increment but also on the relative size of $r$ and $h$ (See Fig. 4.3 (ii)).

   b. If $r$ is measured with an accuracy of $\pm 1 \%$ and $h$ with an accuracy of $\pm 0.5 \%$, about how accurately can $V$ be calculated from the formula $V=\pi r^{2} h$ ?

   Solution

   For $V=\pi r^{2} h$ or $\log V=\log \pi+2 \log r+\log h$, increment approximation implies

   $$\frac{\Delta V}{V} \approx 2 \frac{\Delta r}{r}+\frac{\Delta h}{h} .$$

   Given, $\left.\quad \begin{array}{l}\frac{\Delta r}{r} \times 100=\pm 1, \\ \frac{\Delta h}{h} \times 100=\pm 0.5=\frac{1}{2}\end{array}\right\}$ so that $\left.\begin{array}{l}\left|\frac{\Delta r}{r}\right| \leq \frac{1}{100} \\ \left|\frac{\Delta h}{h}\right| \leq \frac{1}{200}\end{array}\right\}$

   $$\therefore\left|\frac{\Delta V}{V}\right| \approx\left|2 \frac{\Delta r}{r}+\frac{\Delta h}{h}\right| \leq 2\left|\frac{\Delta r}{r}\right|+\left|\frac{\Delta h}{h}\right|=\frac{2}{100}+\frac{1}{200}=0.025$$

   Thus, the maximum percentage error (or change), viz. $\left|\frac{\Delta V}{V}\right| \times 100$, due to possible percentage error (or change) in measurement of $r$ and $A$ will be about $2.5$ per cent.

   c. The period $T$ of a simple pendulum is $T=2 \pi \sqrt{\frac{l}{g}}$, find the maximum percentage error in $T$ due to possible errors up to $1 \%$ in $l$ and $2 \%$ in $g$ (Hint: $\frac{d l}{l}=0.001$ and $\frac{d g}{g}=0.002$ )

   Solution

   $$\begin{aligned} \log T & =\log 2\pi +\frac{1}{2}\log l-\frac{1}{2}\log g\\ \frac{dT}{T} & =0+\frac{1}{2l} dl-\frac{1}{2g} dg\\ & =\left(\frac{1}{2}\right)\left(\frac{dl}{l}\right) -\left(\frac{1}{2}\right)\left(\frac{dg}{g}\right)\\ & =\left(\frac{1}{2}\right)( 0.001) \pm \left(\frac{1}{2}\right)( 0.002)\\ & =0.0005\pm 0.001 \end{aligned}$$

   $$\therefore \text{Max error} =\ 1.5\%$$

   d. The range $R$ of a projectile which starts with a velocity $v$ at an elevation $\alpha$ is given by $R=$ $\frac{v^{2} \sin 2 \alpha}{g}$. Find the percentage error in $R$ due to an error of $1 \%$ in $\mathrm{v}$ and an error of $0.5 \%$ in $\alpha$.

   Solution

   Given $R=\frac{v^{2} \sin 2 \alpha}{g}$ or $\log R=2 \log v+\log \sin 2 \alpha-\log g$.

   By error approximation (i.e. taking differential on both sides)

   $$\frac{\delta R}{R}=2 \frac{\delta v}{v}+\frac{1}{\sin 2 \alpha} \cos 2 \alpha \cdot 2 \delta \alpha,(\delta g=0)$$

   or

   $$\begin{aligned} \left(\frac{\delta R}{R} \times 100\right) &=2\left(\frac{\delta v}{v} \times 100\right)+2 \alpha(\cot 2 \alpha)\left(\frac{\delta \alpha}{\alpha} \times 100\right) \\ &=2 \times 1+2 \alpha \cdot \cot 2 \alpha \times 0.5=2+2 \alpha \cot 2 \alpha \times \frac{1}{2} \\ &=(2+\alpha \cot 2 \alpha) \end{aligned}$$

   Hence, the percentage error in calculation of $R$ due to errors of $1 \%$ in $R$ and $0.5 \%$ in $\alpha$ is $(2+\alpha \cot 2 \alpha)$.

9. Find the equations of the tangent plane and normal line to the following surfaces at the points indicated:

   a. $x^{2}+2 y^{2}+3 z^{2}=6$ at $(1,1,1)$

   Solution

   Partial derivation yields:

   $\frac{\partial f}{\partial x} =2x\quad \quad \frac{\partial f}{\partial y} =4y\quad \quad \frac{\partial f}{\partial z} =6z$

   $\Longrightarrow \ \frac{\partial f}{\partial x}_{( 1,1,1)} =2\quad \quad \frac{\partial f}{\partial y}_{( 1,1,1)} =4\quad \quad \frac{\partial f}{\partial z}_{( 1,1,1)} =6$

   Tangent plane:

   $$\begin{aligned} ( x-x_{o})\left(\frac{\partial f}{\partial x}\right)_{0} +( y-y_{0})\left(\frac{\partial f}{\partial y}\right)_{0} +( z-z_{0})\left(\frac{\partial f}{\partial z}\right)_{0} & =0\\ 2( x-1) +4( y-1) +6( z-1) & =0\\ 2x-2+4y-4+6z-6 & =0\\ x+2y+3z & =6 \end{aligned}$$

   Normal line:

   $$\begin{aligned} \frac{x-x_{0}}{\left(\frac{\partial f}{\partial x}\right)_{0}} & =\frac{y-y_{0}}{\left(\frac{\partial f}{\partial y}\right)_{0}} =\frac{z-z_{0}}{\left(\frac{\partial f}{\partial z}\right)_{0}}\\ \frac{x-1}{2} & =\frac{y-1}{4} =\frac{z-1}{6}\\ \frac{x-1}{1} & =\frac{y-1}{2} =\frac{z-1}{3} \end{aligned}$$

   b. $2 x^{2}+y^{2}-z^{2}=-3$ at $(1,2,3)$

   Solution

   Partial derivation yields:

   $\frac{\partial f}{\partial x} =4x\quad \quad \frac{\partial f}{\partial y} =2y\quad \quad \frac{\partial f}{\partial z} =-2z$

   $\Longrightarrow \ \frac{\partial f}{\partial x}_{( 1,2,3)} =4\quad \quad \frac{\partial f}{\partial y}_{( 1,2,3)} =4\quad \quad \frac{\partial f}{\partial z}_{( 1,2,3)} =-6$

   Tangent plane:

   $$\begin{aligned} ( x-x_{o})\left(\frac{\partial f}{\partial x}\right)_{0} +( y-y_{0})\left(\frac{\partial f}{\partial y}\right)_{0} +( z-z_{0})\left(\frac{\partial f}{\partial z}\right)_{0} & =0\\ 4( x-1) +4( y-2) -6( z-3) & =0\\ 4x-4+4y-8-6z+18 & =0\\ 4x+4y-6z & =-6\\ 2x+2y-3z & =-3 \end{aligned}$$

   Normal line:

   $$\begin{aligned} \frac{x-x_{0}}{\left(\frac{\partial f}{\partial x}\right)_{0}} & =\frac{y-y_{0}}{\left(\frac{\partial f}{\partial y}\right)_{0}} =\frac{z-z_{0}}{\left(\frac{\partial f}{\partial z}\right)_{0}}\\ \frac{x-1}{4} & =\frac{y-2}{4} =\frac{z-3}{-6}\\ \frac{x-1}{2} & =\frac{y-2}{2} =\frac{z-3}{-3} \end{aligned}$$

   c. $x^{2}+y^{2}-z=1$ at $(1,2,4)$

   Solution

   Partial derivation yields:

   $\frac{\partial f}{\partial x} =2x\quad \quad \frac{\partial f}{\partial y} =2y\quad \quad \frac{\partial f}{\partial z} =-1$

   $\Longrightarrow \ \frac{\partial f}{\partial x}_{( 1,2,4)} =2\quad \quad \frac{\partial f}{\partial y}_{( 1,2,4)} =4\quad \quad \frac{\partial f}{\partial z}_{( 1,2,4)} =-1$

   Tangent plane:

   $$\begin{aligned} ( x-x_{o})\left(\frac{\partial f}{\partial x}\right)_{0} +( y-y_{0})\left(\frac{\partial f}{\partial y}\right)_{0} +( z-z_{0})\left(\frac{\partial f}{\partial z}\right)_{0} & =0\\ 2( x-1) +4( y-2) -1( z-4) & =0\\ 2x-2+4y-8-z+4 & =0\\ 2x+4y-z & =6 \end{aligned}$$

   Normal line:

   $$\begin{aligned} \frac{x-x_{0}}{\left(\frac{\partial f}{\partial x}\right)_{0}} & =\frac{y-y_{0}}{\left(\frac{\partial f}{\partial y}\right)_{0}} =\frac{z-z_{0}}{\left(\frac{\partial f}{\partial z}\right)_{0}}\\ \frac{x-1}{2} & =\frac{y-2}{4} =\frac{z-4}{-1} \end{aligned}$$

   d. $\displaystyle \ln \left(\frac{x}{y}\right)-z^{2}(x-2 y)-3 z=3$ at $(4,2,-1)$

   Solution

   Partial derivation yields:

   $\frac{\partial f}{\partial x} =\frac{1}{x} -z^{2} \quad \quad \frac{\partial f}{\partial y} =2z^{2} -\frac{1}{y} \quad \quad \frac{\partial f}{\partial z} =-2z( x-2y) -3$

   $\Longrightarrow \ \frac{\partial f}{\partial x}_{( 4,2,-1)} =-\frac{3}{4} \quad \quad \frac{\partial f}{\partial y}_{( 4,2,-1)} =\frac{3}{2} \quad \quad \frac{\partial f}{\partial z}_{( 4,2,-1)} =-3$

   Tangent plane:

   $$\begin{aligned} ( x-x_{o})\left(\frac{\partial f}{\partial x}\right)_{0} +( y-y_{0})\left(\frac{\partial f}{\partial y}\right)_{0} +( z-z_{0})\left(\frac{\partial f}{\partial z}\right)_{0} & =0\\ -\frac{3}{4}( x-4) +\frac{3}{2}( y-2) -3( z+1) & =0\\ -\frac{3}{4} x+3+\frac{3}{2} y-3-3z-3 & =0\\ -\frac{3}{4} x+\frac{3}{2} y-3z & =3 \end{aligned}$$

   Normal line:

   $$\begin{aligned} \frac{x-x_{0}}{\left(\frac{\partial f}{\partial x}\right)_{0}} & =\frac{y-y_{0}}{\left(\frac{\partial f}{\partial y}\right)_{0}} =\frac{z-z_{0}}{\left(\frac{\partial f}{\partial z}\right)_{0}}\\ \frac{x-4}{-\frac{3}{4}} & =\frac{y-2}{\frac{3}{2}} =\frac{z+1}{-3} \end{aligned}$$

   e. $x^{3} z+z^{3} x-2 y z=0$ at $(1,1,1)$

   Solution

   Partial derivation yields:

   $\frac{\partial f}{\partial x} =3x^{2} z+z^{3} \quad \quad \frac{\partial f}{\partial y} =-2z\quad \quad \frac{\partial f}{\partial z} =x^{3} +3z^{2} x-2y$

   $\Longrightarrow \ \frac{\partial f}{\partial x}_{( 1,1,1)} =4\quad \quad \frac{\partial f}{\partial y}_{( 1,1,1)} =-2\quad \quad \frac{\partial f}{\partial z}_{( 1,1,1)} =2$

   Tangent plane:

   $$\begin{aligned} ( x-x_{o})\left(\frac{\partial f}{\partial x}\right)_{0} +( y-y_{0})\left(\frac{\partial f}{\partial y}\right)_{0} +( z-z_{0})\left(\frac{\partial f}{\partial z}\right)_{0} & =0\\ 4( x-1) -2( y-1) +2( z-1) & =0\\ 4x-4-2y+2+2z-2 & =0\\ 4x-2y+2z & =4\\ 2x-y+z & =2 \end{aligned}$$

   Normal line:

   $$\begin{aligned} \frac{x-x_{0}}{\left(\frac{\partial f}{\partial x}\right)_{0}} & =\frac{y-y_{0}}{\left(\frac{\partial f}{\partial y}\right)_{0}} =\frac{z-z_{0}}{\left(\frac{\partial f}{\partial z}\right)_{0}}\\ \frac{x-1}{4} & =\frac{y-1}{-2} =\frac{z-1}{2}\\ \frac{x-1}{2} & =\frac{y-1}{-1} =\frac{z-1}{1} \end{aligned}$$

   f. $z=5+(x-1)^{2}+(y+2)^{2}$ at $(2,0,10)$

   Solution

   $z=5+( x-1)^{2} +( y+2)^{2} \Longrightarrow ( x-1)^{2} +( y+2)^{2} -z=5$

   Partial derivation yields:

   $\frac{\partial f}{\partial x} =2( x-1) \quad \quad \frac{\partial f}{\partial y} =2( y+2) \quad \quad \frac{\partial f}{\partial z} =-1$

   $\Longrightarrow \ \frac{\partial f}{\partial x}_{( 2,0,10)} =2\quad \quad \frac{\partial f}{\partial y}_{( 2,0,10)} =4\quad \quad \frac{\partial f}{\partial z}_{( 2,0,10)} =-1$

   Tangent plane:

   $$\begin{aligned} ( x-x_{o})\left(\frac{\partial f}{\partial x}\right)_{0} +( y-y_{0})\left(\frac{\partial f}{\partial y}\right)_{0} +( z-z_{0})\left(\frac{\partial f}{\partial z}\right)_{0} & =0\\ 2( x-2) +4( y) -( z-10) & =0\\ 2x-4+4y-z+10 & =0\\ 2x+4y-z & =-6 \end{aligned}$$

   Normal line:

   $$\begin{aligned} \frac{x-x_{0}}{\left(\frac{\partial f}{\partial x}\right)_{0}} & =\frac{y-y_{0}}{\left(\frac{\partial f}{\partial y}\right)_{0}} =\frac{z-z_{0}}{\left(\frac{\partial f}{\partial z}\right)_{0}}\\ \frac{x-2}{2} & =\frac{y}{4} =\frac{z-10}{-1} \end{aligned}$$

   g. $\displaystyle\frac{x^{2}}{12}+\frac{y^{2}}{6}+\frac{z^{2}}{4}=1$ at $(1,2,1)$

   Solution

   Partial derivation yields:

   $\frac{\partial f}{\partial x} =\frac{x}{6} \quad \quad \frac{\partial f}{\partial y} =\frac{y}{3} \quad \quad \frac{\partial f}{\partial z} =\frac{z}{2}$

   $\Longrightarrow \ \frac{\partial f}{\partial x}_{( 1,2,1)} =\frac{1}{6} \quad \quad \frac{\partial f}{\partial y}_{( 1,2,1)} =\frac{2}{3} \quad \quad \frac{\partial f}{\partial z}_{( 1,2,1)} =\frac{1}{2}$

   Tangent plane:

   $$\begin{aligned} ( x-x_{o})\left(\frac{\partial f}{\partial x}\right)_{0} +( y-y_{0})\left(\frac{\partial f}{\partial y}\right)_{0} +( z-z_{0})\left(\frac{\partial f}{\partial z}\right)_{0} & =0\\ \frac{1}{6}( x-1) +\frac{2}{3}( y-2) +\frac{1}{2}( z-1) & =0\\ \frac{1}{6} x-\frac{1}{6} +\frac{2}{3} y-\frac{4}{3} +\frac{1}{2} z-\frac{1}{2} & =0\\ \frac{1}{6} x+\frac{4}{6} y+\frac{3}{6} z-\frac{1}{6} -\frac{8}{6} -\frac{3}{6} & =0\\ \frac{1}{6} x+\frac{4}{6} y+\frac{3}{6} z-2 & =0\\ x+4y+3z & =12 \end{aligned}$$

   Normal line:

   $$\begin{aligned} \frac{x-x_{0}}{\left(\frac{\partial f}{\partial x}\right)_{0}} & =\frac{y-y_{0}}{\left(\frac{\partial f}{\partial y}\right)_{0}} =\frac{z-z_{0}}{\left(\frac{\partial f}{\partial z}\right)_{0}}\\ \frac{x-1}{\frac{1}{6}} & =\frac{y-2}{\frac{2}{3}} =\frac{z-1}{\frac{1}{2}}\\ \frac{x-1}{\frac{1}{6}} & =\frac{y-2}{\frac{4}{6}} =\frac{z-1}{\frac{3}{6}}\\ \frac{x-1}{1} & =\frac{y-2}{4} =\frac{z-1}{3} \end{aligned}$$

   h. $z e^{x}+e^{z+1}+x y+y=3$ at $(0,3-1)$

   Solution

   Partial derivation yields:

   $\frac{\partial f}{\partial x} =ze^{x} +y\quad \quad \frac{\partial f}{\partial y} =x+1\quad \quad \frac{\partial f}{\partial z} =e^{x} +e^{z+1}$

   $\Longrightarrow \ \frac{\partial f}{\partial x}_{( 0,3,-1)} =2\quad \quad \frac{\partial f}{\partial y}_{( 0,3,-1)} =1\quad \quad \frac{\partial f}{\partial z}_{( 0,3,-1)} =2$

   Tangent plane:

   $$\begin{aligned} ( x-x_{o})\left(\frac{\partial f}{\partial x}\right)_{0} +( y-y_{0})\left(\frac{\partial f}{\partial y}\right)_{0} +( z-z_{0})\left(\frac{\partial f}{\partial z}\right)_{0} & =0\\ 2( x) +( y-3) +2( z+1) & =0\\ 2x+y-3+2z+2 & =0\\ 2x+y+2z & =1 \end{aligned}$$

   Normal line:

   $$\begin{aligned} \frac{x-x_{0}}{\left(\frac{\partial f}{\partial x}\right)_{0}} & =\frac{y-y_{0}}{\left(\frac{\partial f}{\partial y}\right)_{0}} =\frac{z-z_{0}}{\left(\frac{\partial f}{\partial z}\right)_{0}}\\ \frac{x}{2} & =\frac{y-3}{1} =\frac{z+1}{2} \end{aligned}$$